Подпространство, критерий подпространства, система образующих, базис и размерность векторного пространства. Примеры
Определение 3.2.Пусть V = (V, +, {w 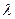 |
| 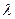
 F}) – векторное пространство. Непустое подмножество L
F}) – векторное пространство. Непустое подмножество L 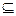 V называется векторным (линейным) подпространством пространства V над полем F, если L само является векторным пространством относительно операций сложения и умножения на скаляр, определенных в пространстве V.
V называется векторным (линейным) подпространством пространства V над полем F, если L само является векторным пространством относительно операций сложения и умножения на скаляр, определенных в пространстве V.
Замечание 3.Из определения следует, что 1) подпространство L определяется над тем же полем, что и пространство V. Справедлива теорема:
Теорема 3.2 (критерий подпространства). Непустое подмножество L 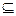 V является векторным подпространством пространства V над полем F, тогда и только тогда, когда L замкнуто относительно операций (+) и
V является векторным подпространством пространства V над полем F, тогда и только тогда, когда L замкнуто относительно операций (+) и 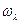 : 1)
: 1)  а, b
а, b  Vа + b
Vа + b  V; 2)
V; 2) 
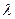
 F
F  а
а  V
V 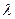 а
а  V.
V.
Примеры: 1.Пусть дано пространство(V3, +, { 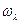 |
| 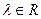 }),его подпространствами будут:
}),его подпространствами будут:
а) (L1, +, { 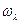 |
| 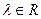 }) –подпространство одномерных векторов,лежащих на любой прямой, проходящей через начало координат;
}) –подпространство одномерных векторов,лежащих на любой прямой, проходящей через начало координат;
б) (L2, +, { 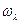 |
| 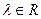 }) –подпространство двумерных векторов,лежащих на плоскости, проходящей через начало координат;
}) –подпространство двумерных векторов,лежащих на плоскости, проходящей через начало координат;
в) (L3 = {a = ( 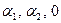 ), где
), где 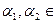 R}, +, {
R}, +, { 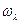 |
| 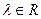 }) –подпространство в R3;
}) –подпространство в R3;
2. Пусть дано векторное пространствоМ22(R) – векторное пространство квадратных матриц 2-го порядка над полем R. Множество L = 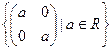 является егоподпространством.
является егоподпространством.
Определение 3.3. Конечная система векторов S = (a1 , … , an)называется линейно зависимой, если существует нетривиальная линейная комбинация её векторов, равная нулевому вектору пространства V . Другими словами, конечная система векторов S линейно зависима, если:
$ a1 , … , an Î F (a1 ¹ 0 Ú … Ú an ¹ 0)Ù (a1× a1 + … + an× an = 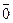 ).
).
Определение 3.4. Конечная система векторов S = (a1 , … , an)называется линейно независимой, если:
" a1 , … , an Î F a1× a1+ … +an× an = 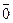 ® a1 = … = an = 0 .
® a1 = … = an = 0 .
Примеры: 1. Система векторов S= ((1, 2, 3), (–2, 3, 1), (–1, 5, 4))в векторном пространстве R3линейно зависима, т.к. 1× a1 + 1× a2 – 1× a3= 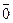 – нетривиальная линейная комбинация, равная нулевому вектору. Эту комбинацию можно найти, записав условие:
– нетривиальная линейная комбинация, равная нулевому вектору. Эту комбинацию можно найти, записав условие:
a1× a1 + a2× a2 + a3× a3 = 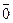
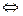 a1 × (1, 2, 3)+a2 × (–2, 3, 1)+a3 × (–1, 5, 4) = (0, 0, 0)и решив соответствующую однородную систему уравнений.
a1 × (1, 2, 3)+a2 × (–2, 3, 1)+a3 × (–1, 5, 4) = (0, 0, 0)и решив соответствующую однородную систему уравнений.
2. Любые коллинеарные или компланарные векторы в векторном пространстве геометрических векторов V3 линейно зависимы.
Определение 3.5.Векторное пространство V над полем F называется конечномерным, если существует такая конечная система S ={a1,…, an} Í V, что любой вектор bÎ Vможно представить в виде линейной комбинации b=a1 × a1 + … + an × an. При этом система векторов (a1, … , an)называется порождающими или образующими векторного пространства V .
Определение 3.5. Конечная система (1) (e1, …, en) векторов пространства V называется базисом векторного пространства V , если одновременно выполнены два условия:
1)система (1)– линейно независима,2) система (1)– система образующих векторного пространства V.
Теорема 3.3 (о базисе конечномерного векторного пространства).
1) Любое ненулевое конечномерное векторное пространство обладает базисом,
2) любые два базиса конечномерного векторного пространства состоят из одинакового числа векторов.
Определение 3.5. Число векторов в любом базисе ненулевого конечномерного векторного пространства V называется его размерностью и обозначается через dim V.
Замечание 4. По определению, считают размерность нулевого векторного пространства равной 0.
Примеры: 1. Векторное пространство геометрических векторов V2 двухмерно (dim V2 = 2). Его базисы – это любые системы из двух неколлинеарных вектора.
2. Векторное пространство геометрических векторов V3 трёхмерно (dimV3 = 3). Его базисы – это любые системы трёх некомпланарных векторов.
3. Арифметическое векторное пространство Rnявляется n-мерным. Его стандартным базисом служит система векторов ei = (0, … , 0, 1, 0, … , 0), где 1 £ i £ n. (dim Rn = n).
4. Векторное пространство решений однородной системы линейных уравнений А × Х = 0, где А Î Mm n(F)имеет размерность n – rg(A). Его базисом будет любая фундаментальная система решений.
Теорема 3.4. Любой вектор b Î V единственным образом разлагается по базису (1)(e1, e2, …, en) конечномерного векторного пространства V, то есть представляется в виде b = a1 × e1 + a2 × e2 + … + an × en.
Определение 3.6.Пусть b= a1 × e1 + a2 × e2 + … + an × en – разложение вектора b по базису (1) векторного пространства V над полем F. Упорядоченный набор чисел (a1, a2, …, an) из поля F называется координатами вектора b в базисе (1).
Пример.В пространстве R3система векторов e1 = (1, 0, 0), e2= (0, 2, 0), e3 = (0, 0, 3) базисом. Вектор а = (2, 4, 9) имеет координаты (2, 2, 3) в этом базисе, так как
b = 2 × e1 + 2 × e2 + 3 × e3.
Дата добавления: 2021-12-14; просмотров: 620;











