Ортогональные базисы евклидовых пространств
Пусть V– конечномерное евклидово пространство, e = (e1 , … , en) – конечная система векторов в V. Система e называется ортогональной, если (ei , ej) = 0 при i ¹ j. Если в дополнение к этому длины всех векторов системы e равны 1, то она называется ортонормированной.
Замечание. Если n = 1, то условие ортогональности не требует ничего, а для ортонормированности необходимо и достаточно, чтобы |e1| = 1.
Примеры: 1. Пусть V = R3 – стандартное евклидово пространство. Тогда система векторов ((1; –1; 0), (1; 1; 0), (0; 0; 1)) является ортогональным, но не ортонормированным базисом, а система векторов
(( 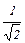 ; –
; – 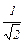 ; 0), (
; 0), ( 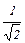 ;
; 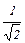 ; 0), (0; 0; 1))
; 0), (0; 0; 1))
является ортонормированным базисом пространства V.
2. Стандартный базис стандартного евклидова пространства ортонормирован.
Замечание. Если базис e = (e1 , … , en ) векторного пространства V ортогонален, то система векторов f = {fi = 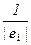 ×ei | 1 £ i £ n } является ортонормированным базисом .
×ei | 1 £ i £ n } является ортонормированным базисом .
В самом деле, система f = (f1 , … , fn) эквивалентна системе e (т.к. каждый её вектор получен умножением соответствующего вектора системы e на ненулевой скаляр). Поэтому f – базис. Кроме того,
(fi , fj) = ( 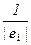 ×ei ,
×ei , 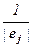 ×ej ) =
×ej ) = 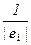 ×
× 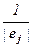 ×(ei , ej ) =
×(ei , ej ) = 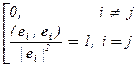 .
.
Таким образом, система f ортогональна и |fi| = 1 (1 £ i £ n), что и требовалось.
Теорема (об ортонормированном базисе).Ненулевое конечномерное евклидово пространство обладает ортонормированным базисом.
Доказательство. Пусть V – ненулевое n-мерное евклидово пространство с базисом e = (e1 , … , en). Проведем индукцию по числу n.
Если n = 1, то f = ( 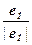 ) – искомый ортонормированный базис.
) – искомый ортонормированный базис.
Предположим, что евклидово пространство с базисом (e2 , … , en) и тем же скалярным произведением, что и V, обладает ортонормированным базисом (f2 , … , fn). Найдём ортонормированный базис для V. Для этого рассмотрим вектор g = e1 – (e1 , f2)×f2 – … – (e1 , fn)×fn . Тогда
(g, fi ) = (e1 – 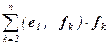 , fi ) = (e1, fi) –
, fi ) = (e1, fi) – 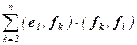 =
=
= (e1 , fi )–(e1 , fi ) = 0,
т.к. (fk , fi ) = dki – символ Кронекера (величина, равная 0 при k ¹ i и 1 – при k = i). Итак, система векторов (g , f2 , … , fn) ортогональна и эквивалентна системе (e1 , f2 , … , fn) – базису пространства V(?!), т.е. является ортогональным базисом V. Осталось заменить gна f1 = 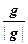 .
.
Теорема доказана.
Пример. Найти ортонормированный базис пространства, порожденного в R4 векторами e1 = (0; 1; 0; –1), e2 = (1; –1; 1; 0), e3 = (1; 0; 0; 1) (скалярное произведение в R4 предполагается стандартным).
Последовательно строим ортонормированный базис, как при доказательстве теоремы. Полагаем f3 = 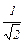 ×e3 =
×e3 = 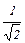 ×(1, 0, 0, 1) и g = e2 – (e2 , f3 )×f3 = = (1; –1; 1; 0) –
×(1, 0, 0, 1) и g = e2 – (e2 , f3 )×f3 = = (1; –1; 1; 0) – 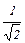 ×
× 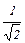 ×(1; 0; 0; 1) = (
×(1; 0; 0; 1) = ( 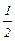 ; –1; 1; –
; –1; 1; – 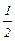 ). Тогда (g , f3 ) = 0, и можно положить f2 =
). Тогда (g , f3 ) = 0, и можно положить f2 = 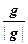 =
= 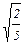 ×g =
×g = 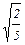 ×(
×( 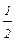 ; –1; 1; –
; –1; 1; – 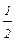 ). Теперь (f2 , f3) – ортонормированная система векторов, эквивалентная (e2 , e3).
). Теперь (f2 , f3) – ортонормированная система векторов, эквивалентная (e2 , e3).
Точно так же, полагаем далее
g = e1 – (e1 , f2 )×f2 – (e1 , f3 )×f3 =
= (0; 1; 0; –1) – 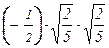 ×(
×( 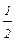 ; –1; 1; –
; –1; 1; – 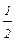 ) –
) – 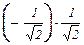 ×(1; 0; 0; 1) =
×(1; 0; 0; 1) =
= (0; 1; 0; –1) + 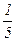 ×(
×( 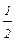 ; –1; 1; –
; –1; 1; – 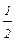 ) +
) + 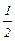
 (1; 0; 0; 1) = (
(1; 0; 0; 1) = (  ;
; 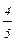 ;
; 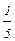 ; –
; –  ).
).
Система (g , f2 , f3 ) ортогональна и, значит, можно взять
f1 = 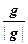 =
= 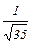 ×(3; 4; 1; –3).
×(3; 4; 1; –3).
Ответ: 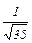 ×(3; 4; 1; –3),
×(3; 4; 1; –3), 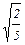 ×(
×( 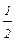 ; –1; 1; –
; –1; 1; – 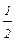 ),
), 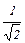 ×(1; 0; 0; 1).
×(1; 0; 0; 1).
Описанный в теореме процесс построения ортогонального базиса, проиллюстрированный примером, называется процессом ортогонализации заданной системы векторов.
Упражнение. Проведите процесс ортогонализации векторов
(1; 2; 0; 0), (0; 2; 1; 0), (0; 0; 1; 2), (0; 0; 2; 1)
в стандартном евклидовом пространстве R4.
Дата добавления: 2021-12-14; просмотров: 543;











