Базис векторного пространства. Координаты вектора

О п р е д е л е н и е. Базисом векторного пространства называется упорядоченная, линейно независимая система векторов такая, что любой вектор пространства можно выразить через векторы этой системы.

О п р е д е л е н и е. Число векторов в базисе называется размерностью векторного пространства.

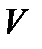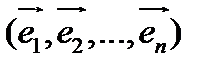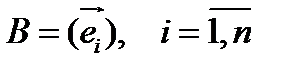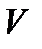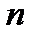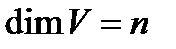Пусть базис векторного пространства состоит из векторов , коротко будем записывать . Размерность векторного пространства равна : . Каждый вектор 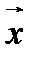векторного пространства можно выразить через векторы базиса: .

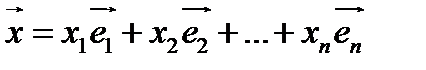О п р е д е л е н и е. Коэффициенты 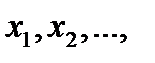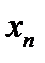в разложении вектора 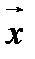по векторам базиса называются координатами вектора .

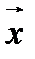У п р а ж н е н и е. Дайте обоснованные ответы на следующие вопросы:

1. Однозначно ли определяются координаты вектора относительно данного базиса?

2. Чему равны координаты суммы векторов?

3. Чему равны координаты произведения вектора на число?

4. Чему равны координаты линейной комбинации векторов?

5. Какова будет размерность векторного пространства, образованного всеми свободными векторами геометрического пространства? Из каких векторов будет состоять любой его базис?

6. Какова будет размерность векторного пространства, образованного всеми свободными векторами, параллельными одной плоскости? Из каких векторов будет состоять любой его базис?

7. Какова будет размерность векторного пространства, образованного всеми свободными векторами, параллельными одной прямой? Из каких векторов будет состоять любой его базис?

8. Как будет выражаться условие коллинеарности свободных векторов через их координаты?