Реалізація булевих формул структурованими ГСА

Якщо просту ГСА, побудовану одним з розглянутих методів, перетворити в дерево, то вона буде структурованою. Цей метод називається методом дублювання. Побудована структурована проста граф-схема алгоритму (СПГСА) містить лише вкладені блоки «повний вибір». Оптимізація числа вершин в цьому випадку забезпечується при побудові її на базі ПГСА з мінімальною кількістю шляхів. На рис. 5.23 наведена СПГСА, побудована за рахунок перетворення граф-схеми вказаного типу (рис. 5.19) в дерево.

Подальша оптимізація СПГСА цього класу за числом вершин досягається за рахунок багатократного «винесення вгору» деяких операторних вершин по графічних правилах (рис. 5.24). На рис. 5.25, рис. 5.26 приведені СПГСА, отримані за рахунок вказаних перетворень граф-схеми (рис. 5.23). Таким чином, викладений підхід дозволяє використовувати в структурі як вкладені блоки «неповний вибір», так і послідовне з'єднання операторних вершин з блоками цього типу.

Оскільки число вершин у СПГСА при використанні даного методу визначається кількістю шляхів, то верхня оцінка кількості вершин в цьому випадку є показовою функцією від числа змінних у формулі, що реалізується.

Подальше розширення варіантів припустимого з'єднання блоків забезпечується при використанні методу незалежних фрагментів, що дозволяє сполучати вкладені конструкції послідовно. Основна перевага методу полягає в тому, що він дозволяє будувати СПГСА за рахунок заміни фрагментів спеціально проектованого аналітичного виразу (об'єднаної формули), що описує її структуру, бібліотечними блоками (рис. 5.27).

Такий підхід близький до побудови паралельно-послідовних контактних схем по логічним формулах в базисі І, АБО, НЕ, але на відміну від останніх вказані аналітичні вирази не описують функціонування СПГСА.

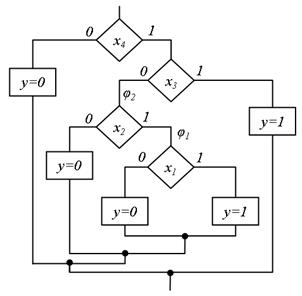
Рис.5.23. Перетворення граф-схеми в дерево

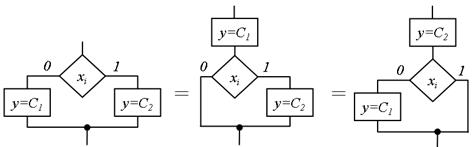
Рис.5.24. Оптимізація за числом вершин

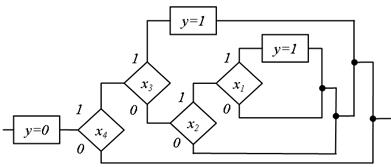
Рис.5.25. Результат перетворення граф-схеми

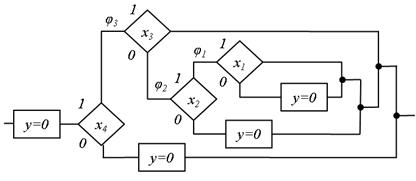
Рис.5.26. Результат перетворення граф-схеми

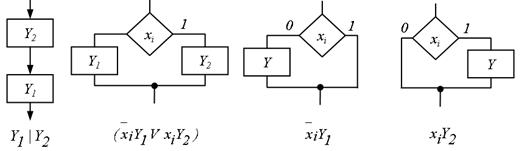
Рис.5.27. Заміна фрагментів аналітичними виразами

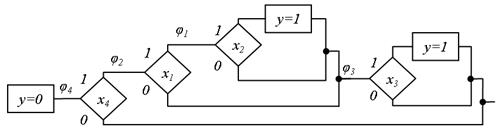
Рис.5.28. В початок СПГСА вводиться операторна вершина

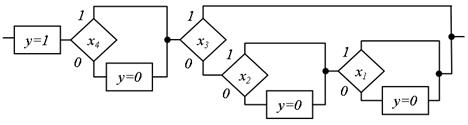
Рис.5.29. Реалізація формули за допомогою додаткової структури

Неструктуровані ПГСА аналогічні контактним схемам, оскільки формули, по яких вони будуються, описують функціонування, але не описують структуру.

Для формули 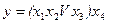вказаний аналітичний вираз будується таким чином. Задана формула записується в бездужковій формі: 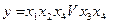будується об'єднана формула, в якій кожна кон'юнкція позначається символом 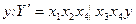. Здійснюється винесення за дужки змінних 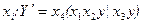, що повторюються, ліворуч. Фрагменти цього виразу замінюються бібліотечними елементами (рис. 5.27), а в початок СПГСА вводиться операторна вершина 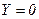(рис. 5.28). При цьому 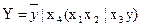. Символу 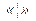в побудованому виразі відповідає послідовне з'єднання блоків в СПГСА. Для цієї мети може бути використаний також символ .

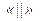Модифікуємо викладений метод для побудови формули за допомогою додаткової структури. При цьому синтез ведеться по інверсії формули. Кон'юнкції в бездужковому виразі позначаються символом 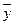, а на початку СПГСА встановлюється вершина 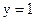. Для даного прикладу 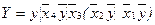. Реалізація заданої формули в цьому випадку наведена на рис. 5.29.

Відзначимо, що при використанні методу незалежних фрагментів послідовно сполучені блоки (окрім блоку початкової установки) допускається міняти місцями. Цей метод може бути використаний також для побудови СПГСА за системою булевих формул. Нехай 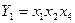, 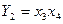. Тоді .

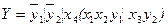Розглянутий метод для однієї формули забезпечує мінімальну нижню оцінку кількості вершин 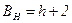і нелінійну верхню оцінку.

Ще один метод структуризації носить назву «Метод булевих ознак». При його використанні для кожної точки об'єднання дуг лінійного ПГСА (за винятком сполученої з операторною вершиною, якщо така точка є) вводиться булева ознака (проміжна змінна). Після цього ПГСА розбивається на фрагменти, які структуруються методом дублювання з введенням додаткових операторних вершин, в яких здійснюється привласнення булевим ознакам значення, рівного одиниці. Фрагменти об'єднуються в СПГСА за допомогою умовних вершин, в яких перевіряються значення булевих ознак. На рис. 5.30 наведена СПГСА, побудована цим методом по ПГСА (рис. 5.18).

Виключити перевірку проміжних змінних, замінивши її перевіркою значень вихідної змінної, вдається в тих випадках, коли при кожному розкладанні Шенона принаймні одна із залишкових формул дорівнює константі.

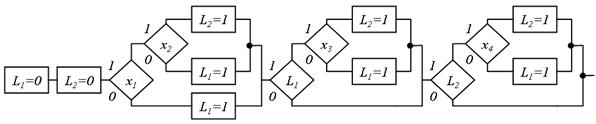Рис.5.30. СПГСА побудована методом мулевих ознак

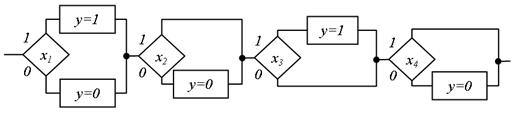
Рис.5.31. Структурована проста граф-схема алгоритму

Метод побудови СПГСА для кожної формули цього класу полягає в побудові лінійної ПГСА і в перетворенні її в структуровану. При цьому ПГСА з максимальною кількістю шляхів читається в зворотньому порядку і по ній формуються h фрагментів, перший з яких є блоком «повний вибір», а останні – блоками «неповний вибір». У кожному блоці використовується одна з умовних вершин лінійної ПГСА. Перший блок за допомогою правила «винесення вгору» (рис. 5.24) завжди може бути перетворений в послідовне з'єднання двох блоків, один з яких є операторною вершиною, а другий – блоком «неповний вибір». Блоки формуються таким чином. Якщо в лінійній ПГСА дуга, що виходить з умовної вершини і не входить в основу, сполучена з «нульовою» («одиничною») операторною вершиною або точкою основи, то відповідна дуга умовної вершини, розташованої в блоці, з'єднується з операторною вершиною .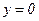

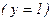Блоки в СПГСА з'єднуються між собою послідовно до тих пір, поки в основі лінійної ПГСА не зустрінеться точка, яка замінюється умовною вершиною, перевіряючи значення вихідної змінної. У СПГСА даної структури передбачається, що операція «вивід» виконується в кінці обчислень. На рис. 5.31 представлена СПГСА, побудована пропонованим методом по формулі 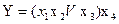. При його використанні по заданій формулі будується лінійна ПГСА (рис. 5.18), яка потім структурується. Ця формула належить даному класу, оскільки при розкладанні Шенона відповідні залишкові формули дорівнюють константам: 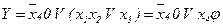; 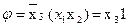, і так далі.

Оцінимо число вершин у ПГСА в цьому випадку. Кількість умовних вершин з незалежними змінними дорівнює h, кількість операторних вершин (OB) – 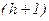, кількість умовних вершин з вихідний змінної – Т, де Т-кількість точок основи, не пов'язаних з операторними вершинами (ОВ). Таким чином .

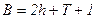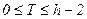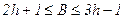Оскільки , то . Кількість вершин у СПГСА (рис. 5.31) відповідає верхній оцінці і дорівнює 11. Якщо по формулі, що реалізовується, будувати лінійну ПГСА з мінімальним числом шляхів, то 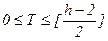. При цьому .

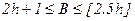З викладеного виходить, що якщо формула може бути реалізована лінійною ПГСА з 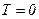, то СПГСА утворюється лише послідовним з'єднанням одного блоку «повний вибір» та 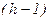-го блоку «неповний вибір». Простою ознакою приналежності формули цьому класу є можливість реалізації однотипної з нею позитивної монотонної формули лінійною схемою з двохвходових елементів І та АБО.

БПФ реалізується послідовною СПГСА, якщо вона записана в порядку незростання вагів її змінних.

Для формули 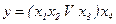послідовна СПГСА (рис. 5.32) будується по лінійній ПГСА (рис. 5.19). При цьому число вершин у СПГСА 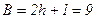Відзначимо, що при використанні пропонованого методу, на відміну від методу незалежних фрагментів, зміна порядку розташування послідовно з’єднаних блоків неприпустимо, і тому він може бути названий методом залежних фрагментів.

СПГСА для БПФ, записаних в порядку не убування вогких коефіцієнтів її змінних, може бути побудована (без попередньої побудови ПГСА) по таблиці істинності за допомогою модифікації канонічного методу.

Пропоновані підходи дозволяють, зокрема, реалізувати позитивно монотонні формули І і АБО лише з однотипних блоків (не рахуючи блоку початкової установки), сполучених послідовно (рис. 5.33, рис. 5.34).

Це забезпечує можливість циклічної реалізації цих формул при простому тілі циклу. Слід розрізняти багатократне виконання ГСА від циклічної реалізації формули, яка у свою чергу може виконуватися багато разів.

Рис.5.32. Послідовна СПГСА

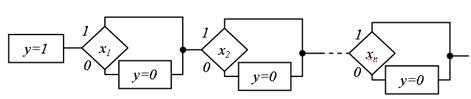
Рис.5.33. Реалізація формул однотипними блоками

Рис.5.34. Реалізація формул однотипними блоками

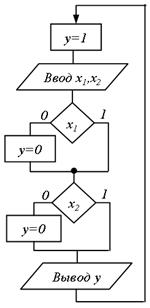
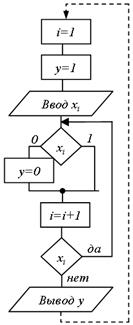
(а) (б)

Рис.5.35. Реалізація формули: а – багатократна, б – однократна та багатократна

Багатократна реалізація ГСА досягається простим замикання її виходу на вхід (поверненням назад), а циклічна реалізація вимагає використання спеціальної конструкції.

На рис. 5.35, а, наведена схема багатократної реалізації формули 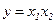, а на рис. 5.35, б – її однократна (без врахування пунктиром) і багатократна (з врахуванням пунктиром) циклічні реалізації, відповідні оператору do-while мови Сі.

Повертаючись до методу залежних фрагментів, відзначимо, що якщо структурована ГСА (СГСА) не обов'язково повинна належати класу простих, то булева формула з пороговим образом може бути реалізована лише послідовним з'єднанням блоків. Для цього задана формула перевизначенням формул зводиться до БПФ меншого числа змінних. Беззворотня порогова формула записується в порядку не зростання вагових коефіцієнтів змінних і реалізується лінійною ГСА, яка в свою чергу перетвориться в СГСА. Неай потрібно реалізувати формулу .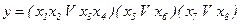

Рис.5.36. Реалізація формули методом залежних фрагментів

Рис.5.37. Реалізація змішаним методом

Перетворимо її до вигляду:

,

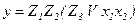де

.

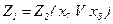
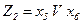
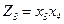Реалізуємо цю формулу методом залежних фрагментів (рис. 5.36). Після зворотної підстановки формул замість змінних 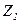, 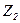і 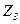отримаємо шуканий СГСА.

Суть змішаного методу полягає в тому, що методом залежних фрагментів будується послідовна СГСА з формулами І та АБО в деяких умовних вершинах незалежних фрагментів, що реалізовуються методом, без використання вершин початкової установки. При цьому, якщо в блоці СГСА використовується оператор 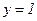, то методом незалежних фрагментів реалізується формулою, а в разі оператора 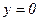за допомогою цього методу будується інверсна формула для здобуття додаткової реалізації.

При застосуванні запропонованого методу для останнього прикладу третій блок в структурі, побудований методом залежних фрагментів, повинен реалізовуватися методом незалежних фрагментів по формулі 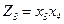, а четвертий і п'ятий блоки – по інверсним формулам: 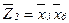і 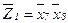(рис. 5.37). Число вершин у побудованій СПГСА дорівнює 14. При використанні методу залежних фрагментів в цьому випадку число вершин дорівнює 20, а для методу незалежних фрагментів – 25 (для прямої реалізації) і 17 (для додаткової). За рахунок ефективнішої реалізації перших двох блоків в СПГСА (рис. 5.37) число вершин може бути скорочено до 13. При цьому вказані блоки замінюються структурою, що описується виразом .

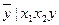Розглянемо ще два методи побудови СГСА для системи булевих функцій. При цьому передбачається, що значення цієї системи задані їх десятковими еквівалентами, тобто система замінена однією функцією, в якій аргументи двійкові, а значення – багатозначні.

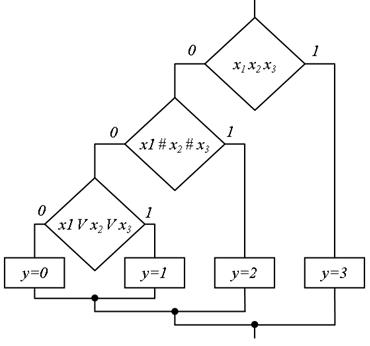
Рис.5.38.

Перший метод будує деревовидну ГСА простої структури, а другий – ГСА, в якій всі блоки «неповний вибір» сполучені послідовно. У цих ГСА в умовних вершинах можуть перевірятися не лише окремі змінні, але і булеві формули.

Перший метод полягає в тому, що в стовпці значень таблиці істинності, що замінює функція, вибирається одне із значень і визначається функція його вибору, що набуває значення, рівного одиниці на вхідних наборах, на яких розташовано вибиране значення, і нуль – на всіх інших наборах. Вибране значення виключається з таблиці істинності, а замінююча функція стає не повністю визначеною, що дозволяє при виборі наступного її значення довизначити функцію вибору до простої. Ця процедура повторюється 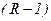разів і будує ГСА, що складається з 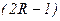вершин, де 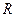– число різних значень в СБФУ.

Реалізуємо як приклад СБФУ з транспонованим стовбцем значень 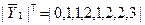при порядку змінних 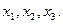Значення 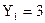вибирає функція 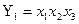. При цьому 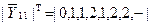. Вибір значення 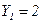здійснимо функцією голосування 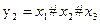При цьому 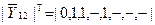. Вибір значень 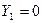і 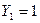здійснює функція 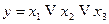. Побудована ГСА представлена на рис. 5.38. Ця схема цікава тим, що реалізація двох булевих формул («голосування» і «сума за модулем два») здійснюється з використанням трьох формул, одна з яких є функцією голосування. Другий метод полягає в тому, що спочатку для замінюючої функції будується основа канонічної таблиці. На основу, в другий ярус, виносяться із стовбців значень таблиці істинності цілі числа, більші за нуль, максимально і однаково зменшуючи значення в кожній парі стовбців, утворюючій кущ канонічної таблиці. Наступні етапи винесення здійснюються аналогічно і проводяться для кожного куща. Після завершення винесення всіх чисел здійснюється багатозначне кодування вершин канонічної таблиці, що полягає в тому, що однакові кущі позначаються однаковими цифрами, а їх нумерація починається від стовпця значень.

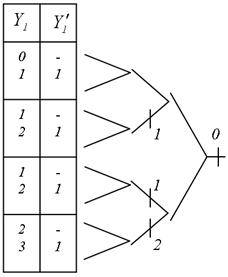
Рис.5.39. Система булевих функцій

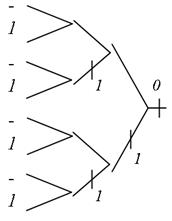
Рис.5.40. Винесення одиниці в третій ярус

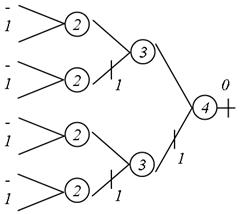
Рис.5.41. Багатозначне кодування вершин канонічної таблиці

Здійснюється об'єднання однойменних кущів і виключаются нульові позначки в перетвореному стовпці значень таблиці істинності. По отриманій канонічній таблиці будується ГСА, замінюючи при цьому цифру 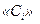на ребрі канонічної таблиці операторних вершиною з позначкою 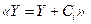. Початкова установка здійснюється за допомогою операторної вершини 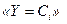, де 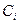– максимальне значення, на яке можуть бути зменшені всі значення стовпця значень таблиці істинності.

Нехай потрібно реалізувати СБФУ, задану стовбцем значень Y₁ (рис. 5.39). На цьому малюнку приведений також спрощений стовпець значень, що одержується з початкового після винесення цілих чисел в канонічній таблиці. На рис. 5.40 виконано винесення одиниці в третій ярус. Багатозначне кодування вершин канонічної таблиці проведене на рис. 5.41. Об'єднання однакових кущів у спрощеній канонічній таблиці показане на рис. 5.42. Структурована ГСА, побудована по цій таблиці, наведена на рис. 5.43.

Якщо ГСА складається лише з послідовного з'єднання операторної вершини 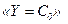і блоків «неповний вибір» з операторними вершинами: 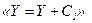, ,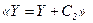..., , 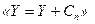то СБФУ, відповідна цій граф-схемі, може бути реалізована лінійним арифметичних поліномом .

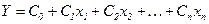З розгляду ГСА (рис. 5.43) виходить, що 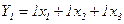, тоді як СБФУ 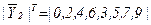реалізується поліномом 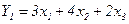(рис. 5.44).

Якщо побудована ГСА має структуру, відмінну від описаної, то СБФУ реалізується нелінійним арифметичним поліномом. На рис. 5.45, б, приведена ГСА, що реалізує СБФУ 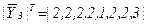запропонованим методом (рис. 5.45, а).

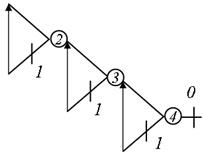
Рис. 5.42. Об'єднання однакових кущів

Рис. 5.43. Структурована ГСА

Рис. 5.44. Реалізація СБФУ поліномом

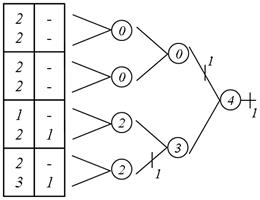
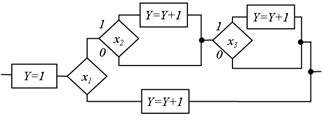
а б
Рис. 5.45. Реалізується нелінійним арифметичним поліномом

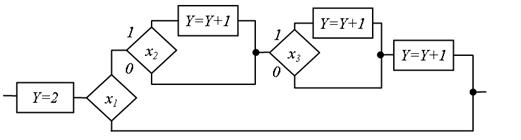
Рис. 5.46.

Рис. 5.47. Реалізація ГСА

Запишемо мінімальне по числу символів арифметичний вираз по цій ГСА: 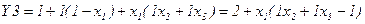. Побудуємо по цьому виразу ГСА (рис. 5.46). Перетворимо отриманий вираз в поліноміальну форму 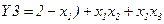і побудуємо по цьому виразу ГСА (рис. 5.47).

З розглянутих прикладів виходить, що довільна СБФУ завжди може бути реалізована структурованою лінійною ГСА із складними умовами і операторними вершинами.