Контроль функціонування автоматів
Автомат з пам'яттю на абстрактному рівні представлення заданий таблицями переходів і виходів. Потрібно синтезувати структурний автомат з виявленням несправностей своєї схеми із заданого класу несправностей при використанні лінійних групових кодів. Інформація на входи автомата надходить без спотворень.
Синтез структурного автомата з контролем здійснюється за правилами канонічного методу структурного синтезу з рядом обмежень на кодування автомата і реалізацію його комбінаційної схеми. Виявлення неправильної роботи автомата забезпечується схемами виявлення помилок (СВП). Кодування станів і виходів автомата з контролем виконується з урахуванням наступних міркувань. Спочатку визначаються максимальні кратності помилок, що виявляють: t1 – у векторах коду станів автомата та t2 – у векторах коду його виходів. Останнє може бути зроблено двома способами: по класу заданих несправностей і припустимій реалізації комбінаційних схем автомата.
В першому випадку вважають, що булеві функції збудження і виходів автомата реалізуються окремо. Тоді заданий клас несправностей однозначно відповідає кратностям t1 і t2 помилок, що виявляються. Наприклад, якщо клас несправностей включає несправності одного будь-якого логічного елемента схеми автомата, то t1= t2=1
В другому випадку припускають у комбінаційних схемах збудження і виходів автомата наявність логічних елементів, що є точками розгалуження, одночасний вихід з ладу яких може привести до появи помилок кратністю не більше i×l у векторах коду станів і помилок кратністю не більше i×т у векторах коду виходів (i – число логічних елементів, одночасний вихід яких з ладу повинен бути виявлений відповідно до заданого класу несправностей; l – сумарне число елементів пам'яті автомата, із входами яких зв'язані i точок розгалуження в комбінаційній схемі (КС) збудження; т – сумарне число виходів автомата, з якими зв'язані i точок розгалуження в КС виходів). При такому виборі повинні виконуватися співвідношення: t1 > i×l та t2 > i×m.
Слід відзначити, що в обох випадках мінімізація кожної булевої функції збудження і функції виходів автомата може здійснюватися будь-якими відомими методами. У другому випадку допускається і спільна мінімізація при збереженні обмежень щодо точок розгалуження.
Далі за отриманим значенням t1 і t2 вибираються лінійні групові коди станів і виходів автомата з відповідними здатностями до виявлення помилок.
До побудованого в такий спосіб автомата додають СВП. Таких схем може бути дві: СВП1 – приєднується до виходів елементів пам'яті автомата і фіксує спотворення інформації у векторах його коду станів; СВП2 – приєднується до вихідних каналів автомата і фіксує спотворення інформації у векторах його коду виходів.
Можна використати тільки одну схему виявлення помилок, а саме СВП2. У цьому випадку булеві функції виходів автомата повинні будуватися з урахуванням ряду особливостей. З розглянутого вище підходу до побудови автомата з контролем роботи витікає, що будь-яка помилка у векторі стану автомата кратності, що не перевищує t1 переводить його в стан, що розташований від правильного на відстані в d £ t1,. Якщо забезпечити в кожному з таких станів (наприклад, у випадку автомата Мура) видачу вихідного сигналу, що не належить коду виходів автомата, то схемою СВП2 таку помилку можна виявити, тому що СВП2 налаштована на фіксацію тільки векторів коду виходів автомата.
Як приклад, розглянемо автомат Мура, заданий таблицею переходів – виходів (табл. 5.22). Синтезуємо структурний автомат з виявленням несправностей одного елемента схеми автомата. Як елементи пам'яті використаємо D-тригери. Для спрощення вважається, що точки розгалуження в комбінаційних схемах автомата відсутні, тобто булеві функції збудження і виходів автомата реалізовані окремо.
Таблиця 5.22.
| Стан автомату | Вхідні сигнали | Вихідні сигнали | |
| x1 | x2 | ||
| y0 y0 y1 y2 |
Оскільки автомат має чотири стани і три вихідних сигнали, то в якості коду станів і коду виходів можна вибрати лінійний груповий код зі здатністю до виявлення помилок t1=t2=t=1, матриця якого має вигляд:
a1 a2 p
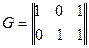
Рівняння, що визначає процедуру декодування, може бути представлене у вигляді:
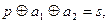
яке фактично визначає структуру схем виявлення помилок СВП1 і СВП2. Кодуємо стани і вихідні сигнали автомата відповідно до обраного коду (табл. 5.23 і табл. 5.24).
Таблиця 5.23. Таблиця 5.24.
| Стан автомата | Код станів | Вихідні сигнали | Код вихідних сигналів | |
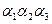
| 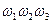
| |||
| y0 y1 y2 |
Структурна таблиця переходів автомата (таблиця функцій збудження) представлена в табл. 5.25.
Таблиця 5.25.
| Стан автомата | Вхідні сигнали | Вихідні сигнали | |
| x1 | x2 | ||
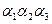
| 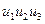
| 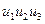
| 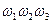
|
Після проведення мінімізації рівняння функцій збудження иi, iÎ{1, 2, 3} і виходів 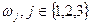 автомата мають вигляд:
автомата мають вигляд:
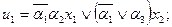
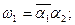
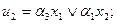
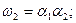
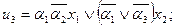
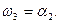
Запишемо рівняння для CВП1: 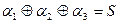 і СВП2:
і СВП2: 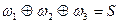 . Структурна схема автомата з контролем представлена на рис.5.78.
. Структурна схема автомата з контролем представлена на рис.5.78.
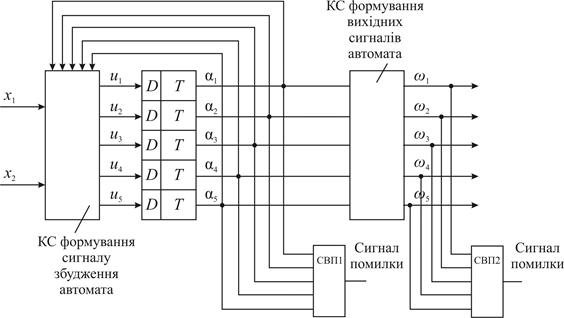
Рис.5.78. Структурна схема автомата з контролем функціонування
Логічний контроль цифрових автоматів з пам'яттю описаний на етапі їх проектування. Можлива ситуація, коли контроль функціонування автомату необхідно забезпечити в розробленому пристрої (за умови, що при розробці пристрою використання контролю не передбачалося). У цьому випадку, як і для комбінаційних схем, необхідно виходити із класу несправностей, що виявляються, і структурної реалізації автомата з пам'яттю. Якщо досить виявляти неправильне функціонування тільки одного елемента схеми автомата (логічний елемент, елемент пам'яті і т.д.), то по наявній принциповій електричній схемі автомата необхідно виявити всі точки розгалуження в КС, що реалізує функції збудження, і КС, що реалізує функції виходу автомата. Максимальна точка розгалуження в КС і дає максимальну кратність помилки, яку необхідно виявляти на виходах КС. Вимоги до кратності помилок, що виявляються, у коді станів і коді виходів автомата можуть бути різними.
Припустимо, є принципова електрична схема автомата з пам'яттю. Потрібно розробити засоби функціонального контролю схеми автомата за умови, що в одиницю часу найбільш ймовірний вихід з ладу тільки одного елемента схеми автомата. На несправності ніяких особливих обмежень не накладається, тобто вважається, що якщо елемент несправний, то він реалізує функцію, відмінну від необхідної. Нехай неправильне функціонування схеми автомата виявляється в момент прояву несправності помилкою або у векторі станів, або у векторі виходів автомата. Дії по реалізації засобів контролю наступні. Насамперед, виходячи із класу розглянутих несправностей потрібно визначити кратність помилки, що підлягає виявленню, у векторах коду станів і коду виходів автомата. Для цього по принциповій електричній схемі автомата виявляються всі максимальні точки розгалуження комбінаційної схеми функцій збудження автомата і комбінаційної схеми виходів автомата. Вважаємо, що в КС функцій збудження є елемент, що впливає на максимальну кратність помилки, яку необхідно виявляти на виходах КС.
Припустимо, що в КС функцій збудження є елемент, що впливає на t1 елементів пам'яті автомата, а в КС виходів – елемент, що впливає на t2, виходів автомата. Тоді для реалізації засобів контролю необхідно, щоб код станів автомата був лінійним груповим кодом з виявленням помилки кратністю t1 а код виходів автомата – лінійним груповим кодом з виявленням помилки кратністю t2. Для побудови лінійних групових кодів з необхідними здатностями до виявлення помилок, необхідно знати код станів і код виходів вихідного автомата, представленого принциповою електричною схемою. Використовуючи принципову електричну схему автомата, а також маючи інформацію про перелік вхідних і вихідних сигналів автомата, нескладно представити функції збудження автомата і його функції виходів в аналітичній формі (у вигляді рівнянь), і по них відновити структурну таблицю переходів автомата. В результаті отримана повна інформація про коди станів і коди виходів автомата. Слід зазначити, що структурна таблиця переходів автомата потрібна для одержання додаткових (перевірочних) функцій збудження і функцій виходів автомата з контролем. Для простоти будемо вважати, що отримані коди станів і виходів автомата мають dmin =1. Оскільки довжина цих кодів відома, то будуємо матриці лінійних групових кодів G1 станіві виходів за правилами побудови лінійних групових кодів. Надалі замінимо вихідну структурну таблицю переходів автомата новою таблицею, в якій кожен стан автомата кодується кодом, заданим за допомогою матриці G1 а кожен вектор виходів автомата — кодом, заданим за допомогою матриці G2.Побудувавши таблицю функцій збудження, синтезуємо самі функції збудження. Функції збудження інформаційної частини лінійного групового коду станів автомата можуть бути реалізовані так само, як і на вихідній принциповій електричній схемі автомата. Функції збудження і функції виходів автомата, що описують перевірочні розряди відповідних завадостійких кодів, повинні реалізуватися заново, наприклад, у вигляді окремого блоку. В загальному випадку, функція збудження перевірочних розрядів і функція виходів є функцією від всіх змінних лінійного групового коду станів і лінійного групового коду виходів автомата. Для реалізації функцій збудження перевірочних розрядів лінійного групового коду станів необхідно мати доступ до виходів елементів пам'яті принципової електричної схеми вихідного автомата.
Нехай функціональна електрична схема автомата задана на рис.5.79.
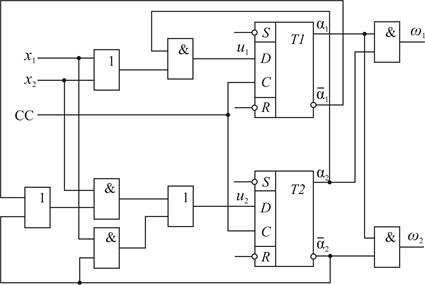
Рис.5.79. Функціональна електрична схема автомата
Розробимо із застосуванням лінійних групових кодів засоби функціонального контролю автомата в класі несправностей одного елемента схеми автомата. Аналіз комбінаційних схем збудження і виходів автомата показує, що точки розгалуження в них відсутні. Отже, кратність помилки, що виявляється у векторах коду станів, повинна бути t1 = 1, а у векторах коду виходів t2 = 1. Виходячи з наявної функціональної схеми одержуємо рівняння функцій збудження:
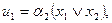
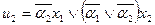 ,
,
і функцій виходів:
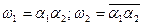 .
.
Відповідно до отриманих рівнянь будуємо структурну таблицю функцій збудження автомата, сполучену з таблицею виходів (табл. 14.8). Оскільки автомат реалізований на D-тригерах, то таблиця переходів збігається з таблицею функцій збудження.
Таблиця 5.26.
| Стан автомата | Вхідні сигнали | Вихідні сигнали | |
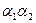
| 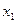
| 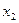
| 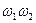
|
Код станів вихідного автомата представляє множину векторів {00, 01, 10, 11}, а код виходів – множину векторів {00, 01, 10}. Матриця, що породжує лінійний груповий код станів з виявленням однократної помилки має вигляд:
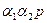
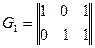
Матриця, що породжує лінійний груповий код виходів з виявленням однократної помилки має вигляд:
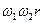
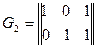 .
.
Рівняння, що визначають структуру схем СВП1 і СВП2 можуть бути представлені в такий спосіб:
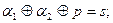
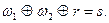
Остаточний варіант структурної таблиці переходів автомата має вигляд (табл. 5.27):
Таблиця 5.27.
| Стан автомату | Вхідні сигнали | Вихідні сигнали | |
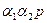
| x1 | x2 | 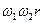
|
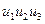
| 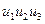
|
Функції збудження і виходів представлені рівняннями:
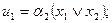
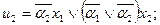
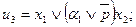
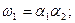
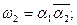
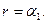
Реалізація схеми автомата з контролем функціонування представлена на рис. 5.80.
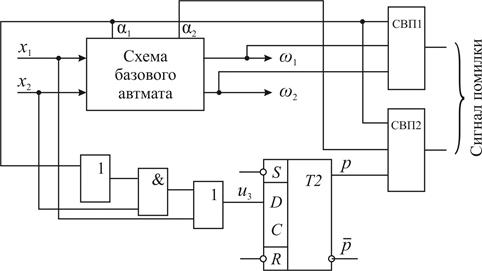
Рис.5.80. Схема автомата з контролем
Дата добавления: 2016-09-26; просмотров: 1565;











