Реалізація автоматів з пам'яттю ГСА

Розгляд цього питання проведемо на прикладі RS-тригера. Якщо автомат заданий у вигляді графу переходів (рис. 5.48), то він може бути ізоморфно змальований у вигляді ГСА (рис. 5.49). Проте ця ГСА вельми незручна для програмування, оскільки вимагає багатократного використання операторів вводу і виводу. Розглянемо питання про побудову ГСА з одним поверненням назад, яка містить лише по одному із вказаних операторів.

Рис.5.48.

Через те що RS-тригер описується формулою 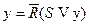, він може бути реалізований операторною ГСА, що представлена на рис. 5.50.

Для побудови СПГСА розкладемо формулу тригера і її залишкові по Шенону (по змінних R та S), або реалізуємо трьохстовбцову таблицю переходів або чотирьохстовбцову кодовану таблицю переходів тригера при вказаному порядку змінних канонічним методом (рис. 5.51). Укрупнимо отриману ГСА, замінивши останній кущ операторною вершиною 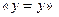і ввівши початкову вершину 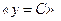(рис. 5.52). Зважаючи на наявність повернення назад вершину 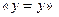в ГСА можна виключити (рис. 5.53).

Тіло побудованої СПГСА складається з вкладених блоків. Використовуємо метод залежних фрагментів для побудови СПГСА, тіло якої складається з послідовно сполучених блоків. Побудуємо лінійну ПГСА по формулі RS-тригера (рис. 5.54). Реалізуємо по цій граф-схемі СПГСА, що складається з послідовності блоків (рис. 5.55). У цій ГСА перший блок може бути виключений. Вводячи блок початкової установки, отримаємо шукану схему (рис. 5.56).

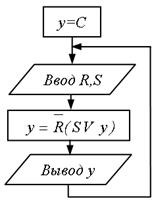
Рис.5.49. ГСА RS-тригера

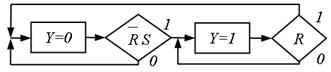
Рис.5.50. Операторна ГСА RS-тригера

Поступаючи аналогічно, побудуємо простіші схеми для RS-тригера (рис. 5.57, рис. 5.58).

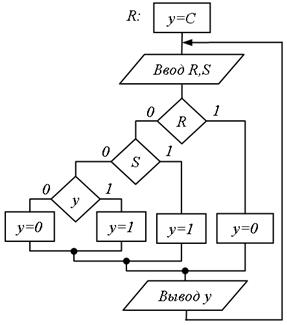
Рис.5.51. Реалізація ГСА канонічним методом

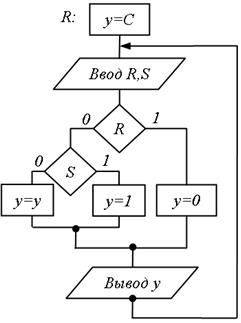
Рис.5.52. Варіант ГСА для RS-тригера

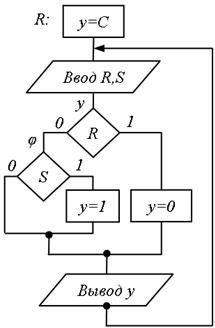
Рис.5.53. Варіант ГСА для RS-тригера

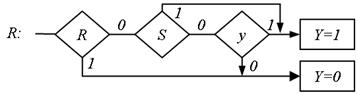
Рис.5.54. Лінійну ПГСА RS-тригера

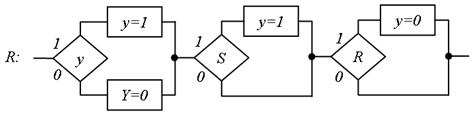
Рис. 4.55. СПГСА, що складається з послідовності блоків

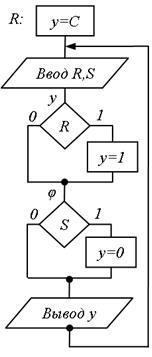
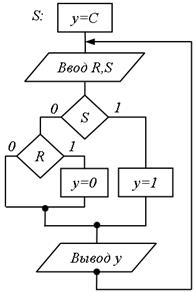
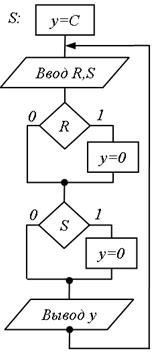
Рис.5.56. Рис.5.57. Рис.5.58.

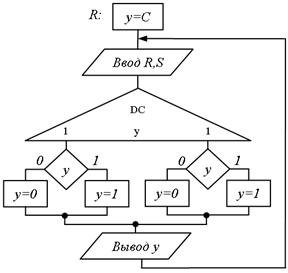
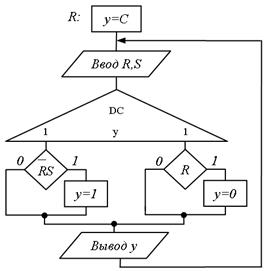
Рис.5.59. Рис.5.60.

Розглянемо ще один підхід до побудови СПГСА. Суть його полягає в тому, що пропонується структура з одним поверненням назад, що дозволяє ізоморфно відобразити вихідний ГП. Тіло СГСА складається з блоку початкової установки, цифрового дешифратора станів з одним входом і s виходами (де s – кількість станів), i-й вихід якого підключений до умовної вершини, виходи якої пов'язані з операторними вершинами, відповідні станам, в які переходить автомат із стану i. На рис. 5.59 представлена схема, побудована по ГП (рис. 5.48). У цій структурі, зважаючи на наявність повернення назад, операторні вершини, що забезпечують збереження попереднього стану, можуть бути виключені (рис. 5.60).

Розглянутий підхід викладений стосовно автомата без вихідного перетворювача, але легко модифікується на інші класи автоматів.

Пропонована структура забезпечує новий (в порівнянні з розглянутими вище) різновид композиції блоків – паралельне з'єднання блоків, кількість яких дорівнює s. При цьому об'єднання блоків здійснюється дешифратором станів, а не вхідними змінними, що різко спрощує «читання» ГСА.більших великих витрат пам'яті, проте він істотно простіший, а схеми більш наочні. Запропонована структура ізоморфна ГП і мовній конструкції switch, що обґрунтовує вживання останньою при програмній реалізації ГСА у випадках, коли жорсткі обмеження на об'єм пам'яті і швидкодію відсутні.

Верифікація ГСА

Верифікація залежно від структури ПГСА здійснюється від виходу до входу, від входу до виходу і спільно, тобто частина фрагментів верифікується від входу до виходу, а останні – від виходу до входу.

Якщо в ПГСА відсутні послідовно сполучені блоки вибору, то вона може бути верифікована від виходу до входу, використовуючи розкладання Шенона для кожної умовної вершини.

Визначимо булеву формулу для лінійної ПГСА (рис. 5.18), читаючи її справа наліво:

;

;
;

.

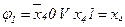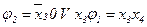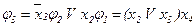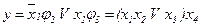Лінійні ПГСА володіють властивістю: на виході кожної умовної вершини реалізується фрагмент заданої формули, а не підформула, що не забезпечується іншими методами.

Визначимо булеву формулу для площинної ПГСА (рис. 5.23), читаючи її від низу до верху:

;

;

;

;

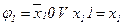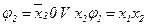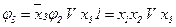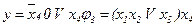Нехай є ГСА для автомата без пам'яті, що реалізує СБФ і що містить послідовно сполучені блоки з одним входом і одним виходом, кожен з яких реалізує одну формулу. Можна стверджувати, що ці блоки не впливають один на одного і тому їх можна аналізувати незалежно, що різко зменшує розмірність вирішуваного завдання. Якщо кожен з цих блоків не містить, в свою чергу, послідовно сполучених блоків, то їх аналіз може проводитися не лише від виходу до входу, але і від входу до виходу.

При цьому спочатку підраховується число одиничних і нульових шляхів в блоці. Якщо число одиничних шляхів в блоці менше, ніж число нульових шляхів, то для кожного одиничного шляху будується відповідна кон'юнкція вхідних змінних. Ці кон'юнкції об'єднуються в диз'юнктивну нормальну форму шуканої формули.

Якщо число нульових шліхів менша, ніж число одиничних шляхів, то дії, вказані вище, виконуються для інверсії формули, по якій надалі будується сама формула.

Отриманий вираз може бути перетворений з метою побудови по ньому нового блоку ГСА з кращими в порівнянні з вихідним блоком характеристиками (число вершин, число шляхів, лінійність і т. д.).

Для ГСА на рис. 5.20 підраховано число одиничних (три) і нульових (п'ять) шляхів. Перерахуємо одиничні шляхи і об'єднаємо їх в диз'юнктивну нормальну форму:

.

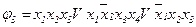Мінімізуємо цю формулу:

.

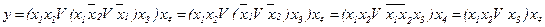Після побудови формули, еквівалентної ГСА (рис. 5.20), є можливість провести етап програмування по цій формулі, а не по граф-схемі, або побудувати лінійну ГСА (рис. 5.18), яка читається краще, ніж початкова.

Якщо СБФ реалізована у вигляді єдиного блоку, то аналіз за допомогою викладених підходів повинен виконуватися для кожної формули окремо.

Побудуємо булеву формулу для площинної ПГСА (рис. 5.27) з «порожніми» дугами:

;

;

;

;

.

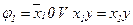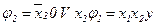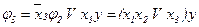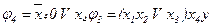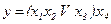Визначимо булеву формулу для автомата з пам'яттю, що реалізовується ПГСА (рис. 5.53):

;

.

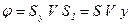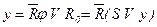Якщо ПГСА складається лише з послідовно сполучених блоків «вибір» (рис. 5.28), то вона верифікується від входу до виходу:

;

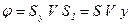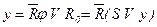
Якщо ПГСА утворена як вкладеними конструкціями, так і послідовним з'єднанням блоків, то перші верифікуються від виходу до входу, а другі – від входу до виходу.

Визначимо булеву формулу для ПГСА (рис. 5.28):

;

;

;

;

.

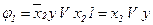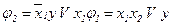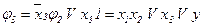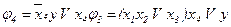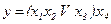Визначимо СБФ для автомата з пам'яттю, що реалізований СПГСА (рис.5.62).

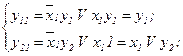
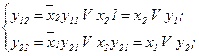
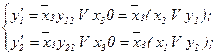
Таким чином, розглянута СПГСА реалізує два RS-триггера – з роздільною установкою і загальним скиданням (рис. 5.61).

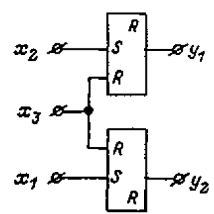
Рис.5.61. Функціональна схема на RS-тригерах

Побудуємо за допомогою методу незалежних фрагментів за умовами переходів RS-тригерів ще одну ГСА для цього прикладу:

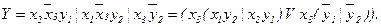
Ця ГСА (рис. 5.63) верифікується аналогічно попередній. В останньому виразі символ 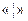позначає послідовне з'єднання блоків в граф-схемі. Розглянемо ще декілька прикладів, в яких ряд кроків здійснюється від виходу до входу (на основі розкладання Шенона), а останні кроки – від входу до виходу (на основі підстановки). На рис. 5.64 приведена ГСА, в якій кожне число, розташоване в квадраті, відповідає порядковому номеру розкладання Шенона. Ця ГСА, що реалізує автомат, описується таким чином:

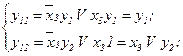
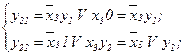
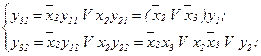
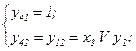
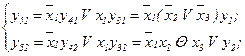
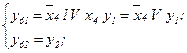
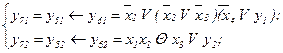
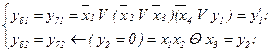
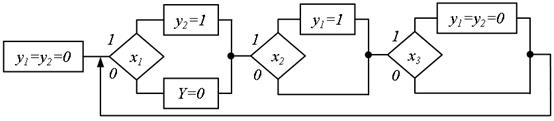
Рис.5.62. СПГСА автомата

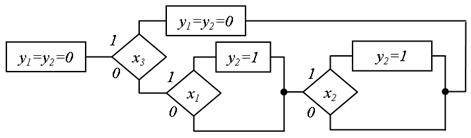
Рис.5.63. ГСА, побудована по формулі

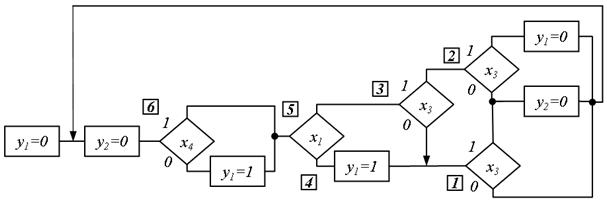
Рис.5.64. Кожне число відповідає порядковому номеру розкладання Шенона

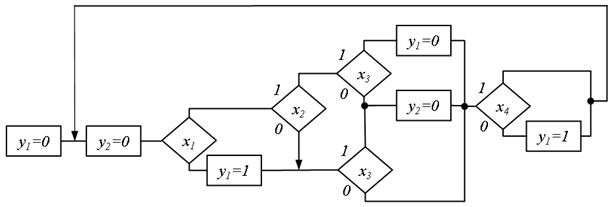
Рис.5.65. Зміна порядку розташування послідовних фрагментів

Зміна порядку розташування послідовних фрагментів в граф-схемі (рис. 5.65) приводить до СБФ вигляду:

; .

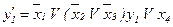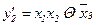Подальша зміна в граф-схемі, пов'язана з перестановкою операторних вершин умовної вершини, поміченою змінною х₃ (рис. 5.66), істотно змінює СБФ, що реалізується:

; .

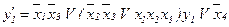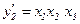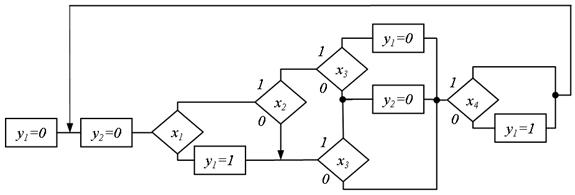
Рис.5.66. Подальша зміна в граф-схемі

Відзначимо, що кожна з розглянутих в останніх трьох прикладах ГСА реалізує або сукупність, що складається з двох автоматів, зв'язаних лише по вхідних змінних (перший з яких є автоматом без вихідного перетворювача з двома станами, а другий – комбінаційною схемою), або один автомат без вихідного перетворювача з чотирма станами, закодованими примусово.

Після проведення змін в ГСА для доказу її правильності повинна виконуватися верифікація – побудова по ГСА системи булевих формул, а по ній у разі потреби граф переходів. Відзначимо, що для ГП автоматів Мура без прапорів і без збереження значень вихідних змінних (без використання умовчань) на відміну від ГСА, локальні зміни структури не можуть привести до глобальної зміни їх поведінки. Верифікація повинна проводитися для доказу правильності побудови ГСА не лише в тих випадках, коли вносяться зміни, але і при «нормальній» їх побудові. Якщо програма побудована без використання ГСА, то остання має бути відновлена по тексту програми для проведення подальшої верифікації.