Аналіз автоматів з JK-тригерами

Синхронізовані скінченні автомати, що будуються на базі JK-тригерів, можуть також синхронізуватись у відповідності до процедури, яка була описана вище. Різниця полягає лише в тому, що необхідно мати два збуджуючих рівняння (Excitation equations) для кожного тригера – одне для J-входу, друге – для входу K-.

Для отримання рівнянь переходів (Transition equations) кожне з них повинно використовувати характеристичне рівняння JK-тригера:

.

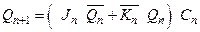На рис. 5.74 приводиться приклад скінченного автомата з використанням JK-тригерів.

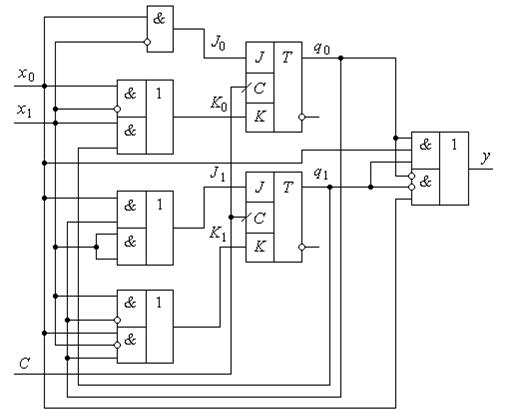
Рис.5.74.

З рис. 5.74 можемо записати наступні рівняння збудження для входів JK-тригерів:

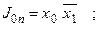
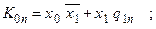
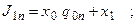
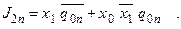
Підставляючи в характеристичне рівняння тригера, отримуємо рівняння переходів:

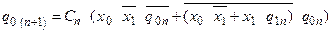;	(5.13)
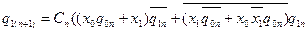
	(5.14)

Таблиця переходів, що базується на цих рівняннях, легко може бути побудована.

Рівняння (5.13) і (5.14) приведемо до досконалої форми:

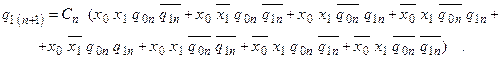
Таблиця станів для обох функцій і має вигляд табл. 5.18, а карти Карно приведені на рис. 5.75.

Таблиця 5.18.

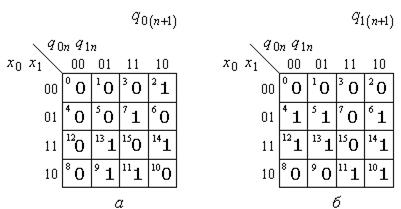
Рис.5.75.

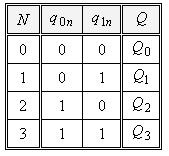
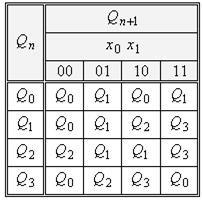
Складаємо таблицю кодування станів (табл. 5.19). Складаємо таблицю переходів (табл. 5.20).

Таблиця 5.19.

Таблиця 5.20.

Будуємо граф-схему переходів (рис. 5.76).

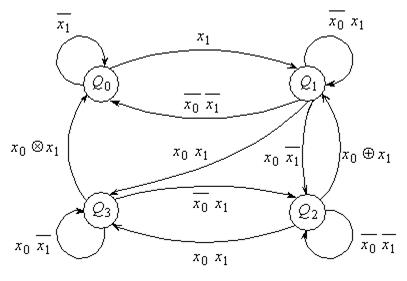
Рис.5.76.

Рівняння, що описує залежність вихідного сигналу, має вигляд:

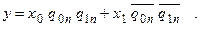
Слід відмітити, що при використанні JK-тригерів можливо використати і інший шлях побудови таблиці переходів. Він полягає в тому, що створюються рівняння збудження і таблиця збудження відносно входів тригерів 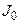, , , , 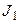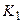які потім використовуються в характеристичних рівняннях кожного тригера при побудові таблиці переходів. Використання такого шляху частково демонструвалося в попередніх прикладах.

Звернемося знову до прикладу схеми двійкового лічильника, що приведена на рис. 5.67, і розглянемо інший варіант його побудови з використання JK-тригерів. Для цього побудуємо таблицю станів з урахуванням сигналів на входах J- і K- кожного тригера і визначимося з логічною функцією 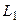, що задаватиме сигнали J і K.

Оскільки нам необхідно мати два тригери, то позначимо їх, як і в схемі-прототипі, – через DD3 і DD4. Відповідні входи тригерів позначимо як 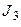, 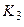і 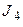, , 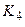а виходи – 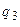і .

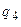Таблиця 5.21.

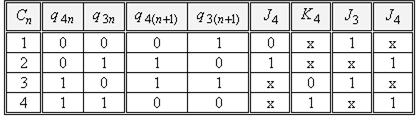
Таблиця будується в такій послідовності. В стовбці 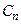задаємо послідовність тактових сигналів. У стовбцях 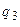і 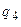задаємо початкові значення виходів тригерів до початку дії синхросигналу і відповідних інформаційних сигналів. Формально в цих стовпцях записується таблиця двійкового коду для двох змінних. У стовбцях 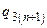і 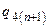записуються значення виходів 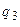і 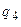після дії синхросигналу в відповідності до табл. 5.4. В стовбцях 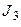, , 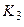, 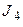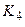записуються ті значення входів, які приведуть до відповідної зміни кодових значень в стовбцях 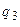і 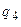. Наприклад: у стовбці 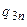до початку дії синхросигналу маємо “0”, а після його дії – “1”. До такої зміни станів тригерів можуть привести сигнали 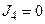, , 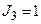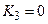. Значення входу 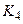– байдуже.

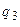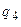Внаслідок побудови таблиці отримуємо залежності між значеннями виходів і від , .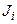

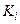Для першого тригера бачимо, що значення 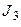і 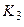мають значення входів, або байдуже, або рівня “1”. Звідси знаходимо, що на його входах постійно може бути присутньою “1”, а, відповідно до алгоритму його роботи, це режим Т-тригера.

Для визначення значень входів 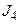і 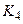також бачимо, що вони можуть бути однаковими, тобто 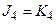, а подальший аналіз зв’язку 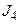з 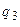приводить до того, що знаходимо 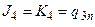. Звідси витікає схема лічильника на JK-тригерах (рис. 5.77).

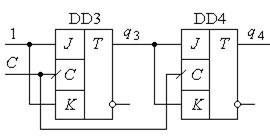
Рис.5.77.

Проаналізуємо його роботу. При поява першого синхроімпульсу приведе до 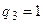; 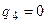. Другий синхроімпульс приведе до зміни стану DD4, тобто 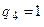, а також до зміни стану DD3: 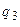зміниться в нуль. Третій синхроімпульс знову приведе до зміни стану 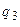з “0” в “1” і, нарешті, четвертий імпульс приведе до обнуління обох тригерів.

Отриманий результат говорить про те, що складність комбінаційної схемотехніки скінченного автомата суттєво залежить від типу використовуваних тригерів. Якщо ж говорити більш точно, то складність комбінаційних схем залежить від уміння розробника використати логічні властивості використовуваних тригерів.