Реалізація булевих формул ГСА

Розглянемо методи побудови простих ГСА (ПГСА) для однієї булевої функції. Називатимемо ГСА простою, якщо вона містить лише умовні вершини, кожна з яких перевіряє одну змінну, і операторні вершини, в яких здійснюється присвоєння констант 0 і 1 вихідний змінній.

Якщо логічна функція задана формулою в базисі І, АБО, НЕ з 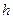літер, то формульний метод дозволяє реалізувати її лінійним ПГСА, що містить 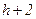вершини, з яких І вершин, – умовні. На рис. 5.18 представлена ПГСА, що реалізовує формулу .

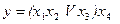Оптимізація лінійної ПГСА за числом шляхів (середній швидкодії) може бути виконана за допомогою метода, суть якого полягає в зміні порядку запису формули, що реалізується. Наприклад, якщо формулу, розглянуту вище, записати як 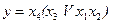і побудувати по ній лінійну ПГСА (рис. 5.19), то число шляхів в ній скорочується. При цьому зменшується також і кількість точок об'єднання дуг графа.

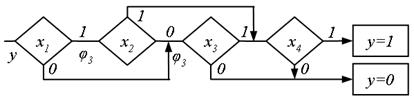
Рис.5.18. ПГСА реалізації булевої формули

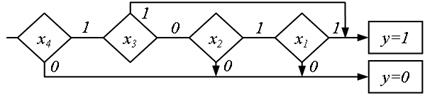
Рис.5.19. ПГСА зі скороченою кількістю шляхів

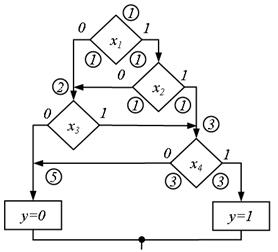
Рис.5.20. Реалізація формули, що побудована канонічним методом

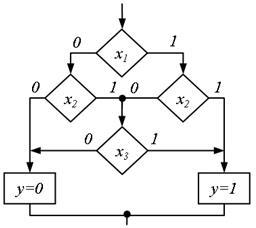
Рис.5.21.

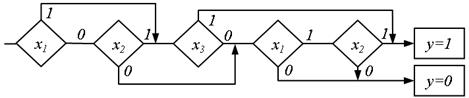
Рис.5.22.

На рис.5.20 наведена ПГСА, що реалізує формулу 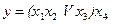яка побудована канонічним методом.

Зміна значень змінних за час проходу одного шляху, що містить однакові перевірки, може бути названо ризиком по аналогії з ризиком в комбінаційних схемах.

Для усунення ризиків необхідно або реалізувати процедуру спілкування з «зовнішнім світом» з використанням буфера, або реалізовувати формулу так, щоб при проходженні одного шляху змінні повторно не опитувалися. Це завжди може бути забезпечено за допомогою методу каскадів або канонічного методу. Відзначимо також, що число шляхів в ГСА при використанні цих методів не більш 2n, тоді як при вживанні формульного методу їх число може бути більше цієї величини.

На рис.5.21 наведена ПГСА, що реалізує формулу 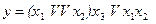за допомогою методу каскадів, а на рис. 5.22 – формульним методом. У першому випадку при чотирьох умовних вершинах кількість шляхів дорівнює шести, а в другому – при п'яти умовних вершинах – одинадцяти.

Для формули в першому випадку ці показники рівні шести і восьми, а в другому – семи і чотирнадцаті.