Аналіз автоматів з D-тригерами

Розглянемо особливості аналізу на конкретних прикладах скінченних автоматів.

Виконаємо аналіз схеми, що приведена на рис. 5.67 і містить вхідну комбінаційну функцію 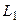, що реалізована на елементах DD1, DD2, вихідну комбінаційну функцію 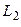, реалізовану на DD5, і модуль пам’яті з використанням динамічних D-тригерів DD3 і DD4. Тобто схема, що розглядається, відноситься до групи автоматів Мілі.

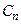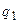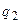Розглянемо поведінку схеми в роботі. За фронтом синхросигналу кожен з тригерів приймає сигнал, що попередньо був поданий на D-вхід, і передає його на свій вихід в відповідності до алгоритму (див. табл. 5.11). Сигнали і є встановлюючими (збуджуючими) для D-тригерів у кожний тактовий момент часу.

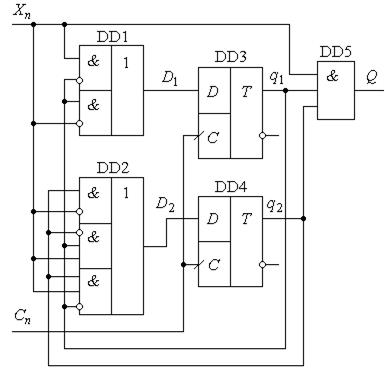
Рис.5.67.

Логічні рівняння, що визначають встановлюючі сигнали як функції поточного стану і вхідних сигналів, називаються збуджуючими рівняннями (Excitation equations) і можуть бути отримані з принципової схеми:

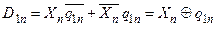;	(5.5)
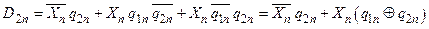.	(5.6)

Функція L₁ , що описується збуджуючими рівняннями, називається функцією збудження.

Використовуючи характеристичні рівняння D-тригерів, можемо записати:

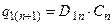;	(5.7)
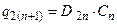.	(5.8)

Підставляючи значення 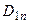, 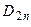з (5.5) – (5.6), отримуємо:

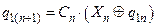;	(5.9)
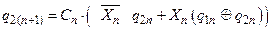.	(5.10)

Отримані рівняння (5.9) – (5.10), що виражають значення стану автомата в (n +1)-й момент часу в залежності від значень його входів і стану в n-й момент часу, називаються перехідними рівняннями. Їх суть полягає в тому, що вони надають можливість передбачити стан автомата в (n +1)-й момент часу на основі інформації про стан і значення входів в n-й момент часу.

Оскільки внутрішній стан автомата визначається значеннями виходів двох тригерів, то можна стверджувати, що існують лише чотири можливі стани автомата: 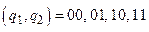. Для кожного стану в приладі, що розглядається, можливі лише два значення вхідного сигналу Х: 0, 1.

В результаті маємо лише вісім комбінацій стан-вхід (у загальному плані автомат з m станами і p вхідними сигналами матиме 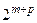комбінацій стан-вхід).

Таблиця 5.11.

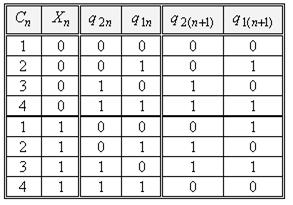
Перехідні рівняння (5.9) – (5.10) можемо задати в табличній формі (див. табл. 5.11). З табл. 5.11 наглядно витікає особливість роботи автомата. Вона полягає в тому, що при 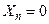автомат не працює, тобто значення вихідних станів в (n +1)-й момент часу повторюють відповідні значення в n-й момент часу. При 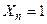він виконує функцію двійкового лічильника з максимальним фіксованим значенням .

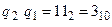Побудуємо тепер на основі Табл. 5.11 таблицю переходів автомата. Для цього кожен з можливих станів автомата позначимо відповідним значенням з множини Q, починаючи з нульового:

; ; ; .

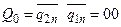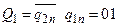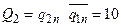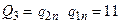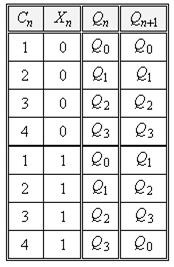
В результаті отримуємо таблицю переходів у вигляді табл. 5.12 або її скорочену форму – табл. 5.13.

Таблиця 5.12.

Таблиця 5.13.

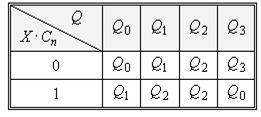
Граф-схема автомата приведена на рис. 5.68. Послідовність переходів з одного стану до іншого забезпечується при наявності динамічного сигналу 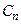від зовнішнього тактового генератора і потенційного (дозволяючого) сигналу x.

Робота автомата може бути описана і за допомогою часових діаграм (рис. 5.69), які відображають зміну станів тригерів автомата (q_1n , q_2n) у відповідні тактові моменти часу, і відповідні стани автомата (Q₀ ÷ Q₃) на кожному тактовому інтервалі.

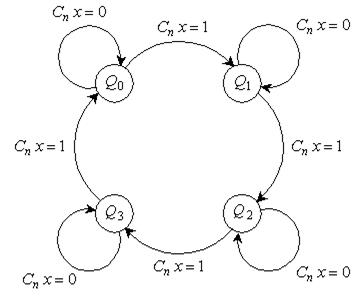
Рис.5.68.

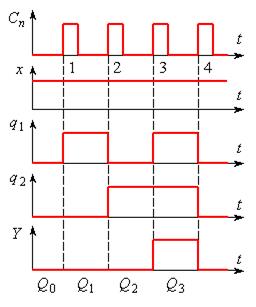
Рис.5.69.

Розглянуту схему автомата можливо спростити за рахунок видалення інверторів, оскільки інверсні значення виходів тригерів можна отримати безпосередньо з тригерів.

Вихідний сигнал автомата визначається внутрішнім його станом і значенням вхідного сигналу, тому функція L₂ описується рівнянням:

.

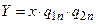Розглянемо ще один приклад. Проаналізуємо роботу скінченного автомата, принципова схема якого приведена на рис. 5.70. Також необхідно побудувати його таблицю станів та часові діаграми роботи.

Із зовнішнього вигляду принципової схеми бачимо, що аналізований автомат відноситься до класу машин Мура, а рівняння для вихідних сигналів y₁ та y₂ мають вигляд:

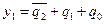;	(5.11)
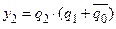.	(5.12)

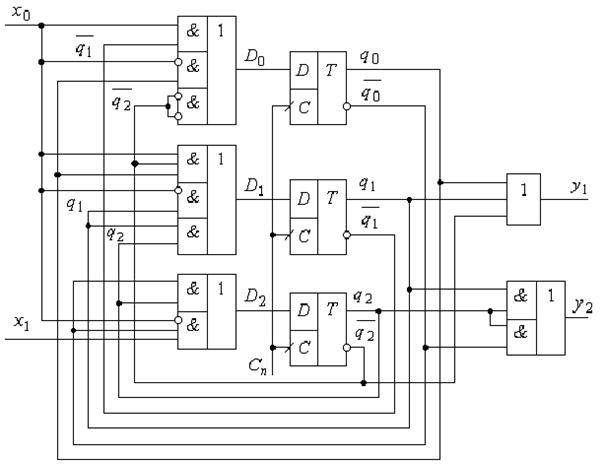
Рис.5.70.

Аналізуючи роботу логічної схеми, можемо записати рівняння збудження тригерів:

^;

;

.

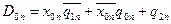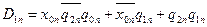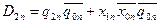Підставляючи рівняння збудження в характеристичне рівняння D-тригерів, отримаємо:

;

;

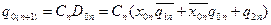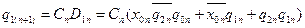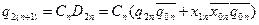
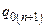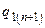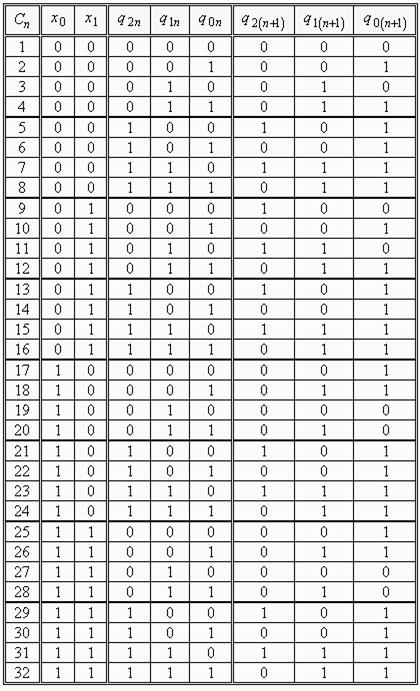
Функції , , 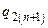зобразимо в табличній формі (див. табл. 5.14).

Таблиця 5.14.

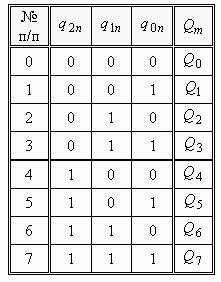
Введемо умовні позначення станів у відповідності до табл. 5.15.

Таблиця 5.15.

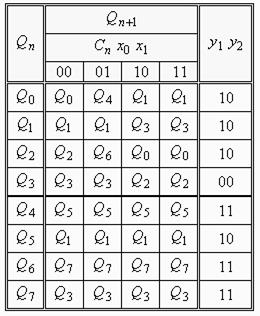
Таблиця 5.16.

Кодування станів дає можливість побудувати таблицю переходів автомата на основі табл. 5.14 (див. табл. 5.16).

На основі таблиці переходів будується граф-схема автомата (рис. 5.71) і аналізуються умови переходів.

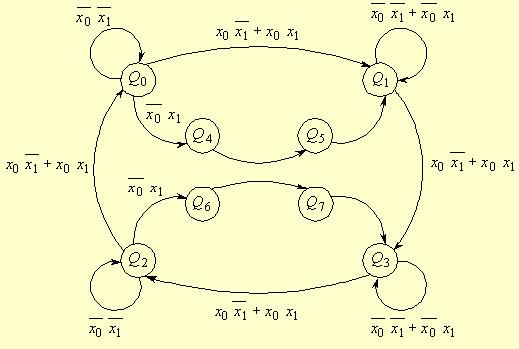
Рис.5.71.

Аналіз роботи автомата на основі граф-схеми з урахуванням керуючих сигналів дає можливість виявити деякі аспекти його роботи. Наприклад, перехід зі стану Q₄ в стан Q₅ забезпечується при всіх значеннях 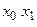і є безумовним. Аналогічно, маємо переходи з Q₅ в Q₁ ; з Q₆ в Q₇ ; з Q₇ в Q₃ .

Звідси витікає, що перехід з Q₀ в Q₄ можна замінити на перехід з Q₀ в Q₁ , а перехід з Q₂ в Q₆ – на перехід з Q₂ в Q₃ . Таблиця переходів при цьому може бути спрощена (див. табл. 5.17), а вигляд граф-схеми відповідатиме рис. 5.72.

Таблиця 5.17.

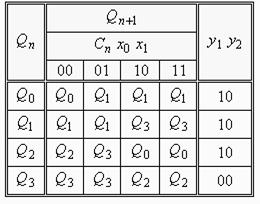
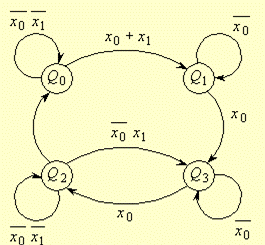Рис.5.72.

Приведений аналіз схеми автомата показує, що при x₁ = 0 матимемо лічильник, який працює у відповідності до коду Грея. При x₁ = 1 виникає можливість забезпечувати своєрідний тригерний режим між станами Q₂ і Q₃ .

Отримані результати дають можливість побудувати часові діаграми роботи автомата. При цьому слід враховувати, що при станах Q₄ ÷ Q₇ має місце y₁ = 1, а y₂ переходить в нуль у стані Q₅ , який є нестійким. Тому можна вважати, що y₂ = 1.

Часові діаграми роботи автомата приведені на рис. 5.73. Часові діаграми виходів y₁ та y₂ не приведені, оскільки вони зрозумілі з формул (5.11), (5.12).

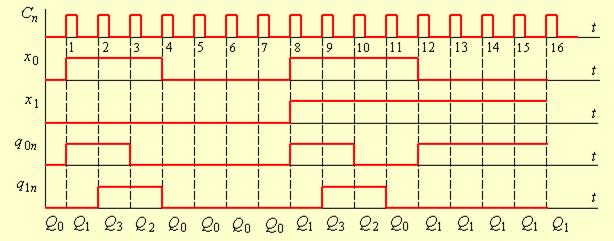
Рис.5.73.