Теорема Котельникова.

Для того, чтобы восстановить исходный непрерывный сигнал из дискретизированного с малыми искажениями (погрешностями), необходимо рационально выбрать шаг дискретизации. Поэтому при преобразовании аналогового сигнала в дискретный обязательно возникает вопрос о величине шага дискретизации Δt. Чем он короче, тем меньше будет отличаться функция u(t) от плавной кривой, проходящей через точки отсчетов. Однако с уменьшением интервала дискретизации Δt возрастает сложность и объем обрабатывающей аппаратуры. При достаточно большом интервале дискретизации Δt возрастает вероятность искажения или потери информации при восстановлении аналогового сигнала.

Оптимальная величина интервала дискретизации устанавливается теоремой Котельникова (другие названия – теорема отсчетов, теорема К. Шеннона, теорема Х. Найквиста; впервые элементы теоремы были отмечены в математике О. Коши, а затем описаны повторно Д. Карсоном и Р. Хартли), доказанной им в 1933 г. Теорема Котельникова имеет важное теоретическое и практическое значение: дает возможность правильно осуществить дискретизацию аналогового сигнала и определяет оптимальный способ его восстановления на приемном конце по отсчетным значениям.

Согласно одной из наиболее известных и простых интерпретаций теоремы Котельникова, произвольный сигнал u(t), спектр которого ограничен некоторой частотой F_B, может быть полностью восстановлен по последовательности своих отсчетных значений, следующих с интервалом времени Δt = 1/2 F_B.

В формулировке В.А.Котельникова (1933 г.) имеются такие слова: «можно непрерывные сигналы передавать с любой точностью при помощи чисел, следующих друг за другом через 0,5/ F_B секунды», т.е. по существу впервые был поставлен вопрос о цифровом способе передачи сигналов. Интервал дискретизации Δt и частоту F_B в радиотехнике иногда называют соответственно интервалом и частотой Найквиста (в отечественной литературе интервал Δt принято называть интервалом Котельникова).

Аналитически теорема Котельникова представляется рядом (впервые такие ряды применил Е.Т. Уттакер в 1915 г. в математической теории интерполяции).

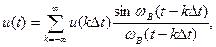
где k – номер отсчета; u(k Δt)—значение непрерывного сигнала в точках отсчета; ω_в= 2π F_B = π/ Δt – верхняя частота спектра сигнала.

Для доказательства теоремы Котельникова рассмотрим произвольный непрерывный сигнал u(t), спектральная плотность S(ω) которого сосредоточена в полосе частот − ω_в ≤ ω ≤ ω_в (сплошная линия на рис. 9.2.)

Тогда

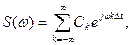
Полагая, что в соотношении [ 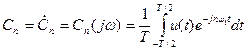] период – это 2ω_В, а интервал дискретизации Δt = π/ ω_В, после подстановки и нескольких преобразований в итоге получим

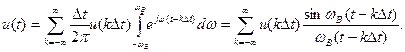
Из этого соотношения следует, что непрерывная функция u(t) действительно определяется совокупностью ее дискретных значений амплитуды в отсчетные моменты времени t = k Δt, что и доказывает теорему Котельникова.

Простейшие сигналы вида

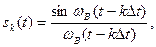
ортогональные друг другу на интервале времени (-∞, ∞), называются функциями отсчетов, базисными функциями, или функциями Котельникова (рис. 9.3). Каждая из базисных функций s_k(t) cдвинута относительно подобной ближайшей функции s_k-1(t) или s_k+1(t) на интервал дискретизации Δt. Анализ последней формулы показывает, что сигнал s_k(t) отражается функцией

sin x/x, которая также характеризует огибающую спектральной плотности прямоугольного импульса. Представление (точнее аппроксимация) заданного непрерывного сигнала u(t) рядом Котельникова иллюстрируется диаграммами на рис. 9.4.

На графике (здесь базисные функции s_k для упрощения показаны без аргумента t) построены четыре первых члена ряда, соответствующие отсчетам сигнала в моменты времени 0, ∆t, 2 ∆t, 3∆t, взятыми в соответствии с теоремой Котельникова. При суммировании этих членов ряда в любые отсчетные моменты времени k∆t, непрерывный сигнал абсолютно точно апроксимируется независимо от числа выбранных отчетов. В интервале же между любыми отчетами сигнал апроксимируется тем точнее, чем больше суммируется членов ряда Котельникова.

Оценка возможности применения теоремы Котельникова к импульсному сигналу u(t) конечной длительности Т_И . Как известно, такие сигналы теоретически обладают бесконечно широким спектром. Однако на практике всегда можно ограничиться некоторой верхней частотой F_B за пределами которой в спектре содержится пренебрежимо малая доля энергии по сравнению с энергией всего исходного сигнала. В радиотехнике таким критерием является содержание 90% средней мощности сигнала в границах спектра. В этом случае сигнал u(t) длительностью Т_И с верхней граничной частотой спектра F_B можетбыть представлен рядом Котельникова с определенным, ограниченным числом отсчетов

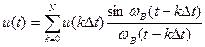(9.1)

Здесь N = T_И/∆t — число отсчетов.

Пример 9.1. Представить рядом Котельникова прямоугольный импульс напряжения единичной амплитуды и длительности τ_и для двух случаев: спектр аппроксимирующей функции ограничен значениями верхней частоты F_B1=1/(2 τ_и) и F_B2=1/ τ_и.

Р е ш е н и е. Для первого случая интервал дискретизации

∆t = 1/(2 F_B)= τ_и, а значит, импульс будет представлен всего двумя отсчетными значениями – в начале и конце импульса. Подставив в (9.1) значения амплитуды и длительности импульса, запишем математическую модель аппроксимирующей функции

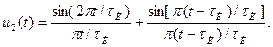
Во втором случае импульс дискретизируется тремя равными отсчетами, производимыми в моменты времени t = 0, τ_и/2 и τ_и , т.е. в начале, середине и конце импульса. Тогда

.

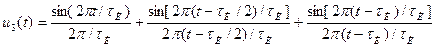Временн'ые диаграммы аппроксимирующих функций u₂(t) и u₃(t) и образующие их члены ряда Котельникова представлены на рис. 9.5.

Пример 9.2. Определить минимальную частоту дискретизации по Котельникову, при которой гармонический сигнал u(t)= cos(kπF₀t + φ₀) может быть полностью восстановлен по своим отчетным значениям (выборкам).

Р е ш е н и е. При выборке интервала дискретизации ∆t = 1/(2 F_B), где F_B – верхняяграничная частота спектра, непрерывный сигнал u(t) можно однозначно восстановить по его отсчетам (Рис. 9.6). Если соотношение частот F₀ < F_B , то к гармоническому сигналу также применима теорема

Котельникова. При этом отсчетные значения данного сигнала

u_k= cos(kπF₀/F_B + φ₀).

В предельном случае, когда частота гармонического сигнала F₀ стремится к частоте дискретизации F_B слева, т.е.

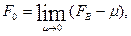
на каждом периоде исходного гармонического сигнала должно осуществляться два отчета. Очевидно, что выборки могут попадать на нулевые значения синусоиды, экстремумы или промежуточные значения. Поскольку априорно фаза выборок относительно синусоиды не известна, то после восстановления сигнала фильтром синусоиду вообще можно не увидеть.

Самая высокая точность восстановления синусоиды будет тогда, когда обе выборки взяты в ее максимальных значениях. При этом колебание на входе ФНЧ имеет пилообразную форму той же частоты, что и частота исходного сигнала (штриховые линии на рис. 9.6)

Если же амплитудные отчеты во времени производятся недостаточно часто и условия теоремы Котельникова нарушаются, то однозначное восстановление исходного гармонического сигнала принципиально невозможно. В этих случаях через отчетные моменты времени можно провести бесчисленное множество кривых, спектральные плотности которых отличны от нуля вне полосы частот −F_B ≤ F ≤ F_B. Поэтому можно утверждать, что погрешность восстановления синусоиды при частоте выборок равной удвоенной частоте синусоиды составляет 100%. Это соответствует теореме Котельникова.

Пример 9.3. Дискретизированный в соответствии с теоремой Котельникова непрерывный сигнал u(t) имеет два отсчета на временн'ой оси.

Вычислить мгновенное значение исходного сигнала в момент времени

t = 1 мкс

Р е ш е н и е. По рисунку определяем, что интервал дискретизации ∆t = 2 ·10-6 с. Отсюда верхняя круговая частота спектра исходного сигнала ωВ = π/∆t= =1,57·106 с-1. Согласно (9.1) ряд Котельникова для данного случая примет вид

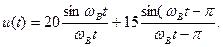
Из этой формулы находим мгновенное значение аналогового сигнала в момент времени t = 1 мкс: u(t=1 мкс)= 22,28 В.