Дискретное преобразование Фурье
Как и при анализе аналоговых сигналов, дискретные сигналы можно представить во временн'ой и частотных областях. В настоящее время обработку дискретных сигналов чаще всего проводят в частотной области, что диктуется значительными сокращениями объема цифровой аппаратуры и времени обработки. Основоположниками способов дискретной и цифровой обработки сигналов считают Голлея (Gooley) и Токе (Tokey), которые предложили в 1965 г. метод дискретного преобразования Фурье (ДПФ).
Пусть дискретной обработке подвергается аналоговый импульсный сигнал u(t) длительностью TИ , имеющий спектральную плотность S(ω) (Рис. 9.10, а, б).
Теоретически можно предположить, что дискретизация сигнала производится периодической последовательностью дельта-функций
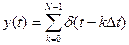 , (9.13)
, (9.13)


где N = TИ/∆t – требуемое число отсчетов, отвечающее теореме Котельникова.
Подставив в (9.10) пределы суммирования от 0 до N – 1, и заменив здесь и далее для упрощения и уменьшения объема формул u(k∆t) = uk, запишем выражение для дискретного сигнала (рис. 9.10, в):
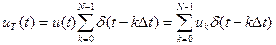 (9.14)
(9.14)
На основании данной формулы можно сделать вывод, что спектр данного дискретного сигнала имеет периодическую структуру с периодом по оси частот ω1 = 2π/Δt (рис. 9.10, г). Мысленно продолжим дискретный сигнал периодически с интервалом ТИ (рис. 9.10, д)
unT(t + nT) = uT(t), n = 0, ±1, ±2,... .
По аналогии с представлением периодических непрерывных сигналов, дискретную функцию unT(t) можно разложить в комплексный ряд Фурье (1.13)
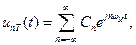 (9.15)
(9.15)
где ωИ = 2π/ТИ = 2 π/NΔt – частота дискретизации спектра дискретного сигнала. Согласно(1.14), комплексные коэффициенты этого ряда:
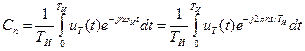 . (9.16)
. (9.16)
Для определения этих коэффициентов проделаем следующее. Подставим формулу (9.14) в (9.16) и, заменив параметр ТИ = NΔt, а также введя безразмерную переменную у = t/Δt, запишем
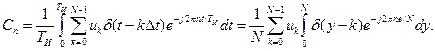
Используя фильтрующее свойство дельта-функции, находим:
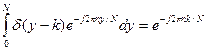 .
.
Тогда окончательная формула для вычисления комплексных коэффициентов ДПФ будет иметь вид:
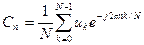 . (9.17)
. (9.17)
Это фундаментальное для дискретных сигналов соотношение, показанное графически на рис. 9.10, е, называется дискретным преобразованием Фурье. (ДПФ). Дискретное преобразование Фурье по существу представляет собой алгоритм вычисления гармонических составляющих спектра Сn по заданным дискретным отчетам uk аналогового сигнала u(t), что значительно сокращает время обработки.
Следует отметить ряд специфических свойств ДПФ, которые нетрудно сформулировать из свойств преобразований Фурье для непрерывных сигналов.
1. Дискретное преобразование Фурье обладает свойством линейности — сумме (разности) дискретных сигналов отвечает сумма (разность) их ДПФ.
2. Коэффициент С0 представляет собой среднее значение (постоянную составляющую) всех дискретных отcчетов сигнала
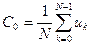 .
.
3. Число определяемых коэффициентов Сn равно числу отсчетов N за длительность сигнала TИ; при n = N коэффициент СN = С0.
ПРИМЕР 9.4. Определить коэффициенты ДПФ дискретизированного прямоугольного импульса единичной амплитуды, заданного четырьмя отсчетами.
Р е ш е н и е . Используя основную формулу (9.17), вычислим коэффициент ДПФ в пределах периода N = 4:
С0 = 4/4 = 1;
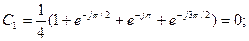
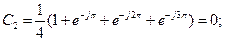
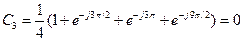 .
.
Таким образом, в пределах периода лишь одна спектральная составляющая с амплитудой 1 отлична от нуля.
Интересно наглядное подтверждение 3-го свойства ДПФ, согласно которому С0 = С4, поскольку 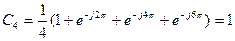 .
.
Дата добавления: 2020-12-11; просмотров: 528;











