Быстрое преобразование Фурье

Многократно сократить число операций позволяет быстрое преобразование Фурье (БПФ), обеспечивающее более скоростное и эффективное цифровое вычисление коэффициентов ДПФ. В основу этого алгоритма положен принцип разбиения (прореживания во времени, или децимации – от греч. деци – доля) заданной последовательности отсчетов дискретного сигнала на ряд промежуточных последовательностей (подпоследовательностей). Это значит, что число дискретов N разделяется на множители (например, N = 8 = 2·2·2, N = 60 = 3·4·5). Затем определяются спектры этих промежуточных последовательностей и через них находится спектр всего сигнала. В зависимости от состава, числа и порядка следования указанных множеств можно создать различные алгоритмы БПФ. В цифровой технике удобнее обрабатывать сигнальные последовательности со значениями числа отсчетов N, являющимися степенью с основанием два (4, 8, 16, и т. д.). Это позволяет многократно делить входную последовательность отсчетов на более мелкие последовательности.

Пусть требуется вычислить ДПФ входной последовательности (массива отcчетов) дискретного сигнала {u(kΔt)} = {u_k}, имеющей четное число отсчетов (рис. 9.11, а), причем N = 2 ^r, где r –целое число (если это условие не выполняется, то последовательность искусственно дополняют нулями до требуемого значения N). Представим входную последовательность в виде двух последовательностей с четными и нечетными номерами и половинным числом членов в каждой (рис. 9.11, а, б, в)

··

u_чт = u_2k; u_нч = u_{2k + 1}; k = 0, 1, 2, ..., N/2 – 1.

Коэффициенты ДПФ для последовательностей с четными и нечетными номерами запишутся отдельно:

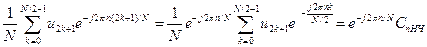
Коэффициенты С_n результирующего ДПФ входной последовательности можно выразить через параметры С_nЧТ и С_nНЧ двух вновь введенных подпоследовательностей. Из последней формулы нетрудно заметить, что в диапазоне номеров отсчетов от 0 до N/2-1 ДПФ входной последовательности определяется соотношением

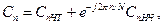n = 0, 1, 2 ..., N/2-1. (9.19)

Так как ДПФ четной и нечетной последовательностей являются периодическими, имеющими период следования N/2, то:

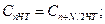
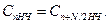
Входящий в формулу (9.19) экспоненциальный множитель при n ≥ N/2 можно записать в виде

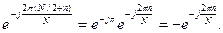
С учетом двух последних выражений находим ДПФ входной последовательности для отсчетов с номерами от N/2 до N-1

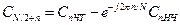, n = 0, 1, 2, ....N/2-1. (9.20) .

Соотношения (9.19) и (9.20) представляют собой алгоритмы БПФ . Отметим, что экспоненциальные фазовые множители 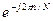в этих алгоритмах учитывают влияние сдвига нечетной последовательности относительно четной.

Cоотношения (9.19) и (9.20) представляют собой алгоритмы БПФ. Следует отметить, что экспоненциальные фазовые множители 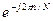в этих алгоритмах учитывают влияние сдвига нечетной подпоследовательности относительно четной.

Чтобы еще уменьшить число вычислений, четную и нечетную подпоследовательности также разбивают каждую на две промежуточные части. Разбиение продолжают вплоть до получения простейших двухэлементных последовательностей. При объединении ДПФ четной и нечетной подпоследовательностей используют алгоритмы (9.19) и (9.20), подставляя в них соответствующие значения номеров N и n.