Спектр дискретного сигнала

Чтобы дать оценку требованиям к длительности дискретизирующих импульсов, нужно определить спектральный состав дискретного сигнала u_T(t). Пусть непрерывный сигнал u(t) имеет спектральную плотность S(ω), (рис. 9.9.).

Последовательность дискретизирующих прямоугольных импульсов у(t) можно представить рядом Фурье, в котором частота ω₁=2π/Δt:

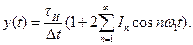(9.3)

Здесь коэффициенты

(9.4)

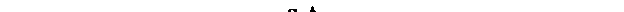
Подставив формулу (9.3) в (9.2), получим

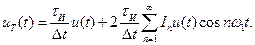(9.5)

Первому слагаемому соответствует спектральная плотность S(ω) исходного сигнала u(t). К произведению u(t)сosnω₁t второго слагаемого можно применить прямое преобразование Фурье. Используя формулу Эйлера и проведя несложные математические выкладки, можно записать

В этом выражении первый интеграл представляет собой спектральную плотность сигнала u(t) на частотах ω – n ω₁, а второй – ту же спектральную плотность, но на частотах ω + n ω₁. Поэтому

(9.6)
Следовательно дискретному сигналу вида (9.6) соответствует спектральная плотность

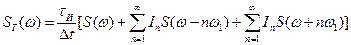(9.7)

Учитывая, что при n=0 коэффициент I_n= 1, можно записать :

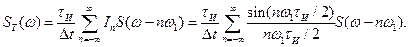(9.8)

График спектра дискретного сигнала, который сформирован из непрерывного, представлен на рис. 9.9.

Полученные результаты позволяют сделать фундаментальные выводы для теории дискретных сигналов.

1. Спектральная плотность S_T(ω) дискретного сигнала u_T(t) представляет собой бесконечную последовательность спектральных плотностей S(ω) исходного непрерывного сигнала u(t), сдвинутых друг относительно друга на частоту дискретизации ω₁;

2. Огибающая спектральной плотности S_T(ω) дискретного сигнала u_T(t) с точностью до коэффициента 1/∆t повторяет огибающую спектральной плотности дискретизирующего прямоугольного импульса.

Чтобы восстановить непрерывный сигнал u(t) из дискретного u_T(t), достаточно выделить центральную часть спектра S_T(ω). Это можно было бы осуществить идеальным ФНЧ, имеющим коэффициент передачи вида штриховой линии прямоугольной формы на рис. 9.9.

К(ω) = К₀; − ω_В≤ ω≤ ω_В. (9.9)

Вместе с тем из курса электротехники известно, что идеальный ФНЧ физически не реализуем и может служить лишь теоретической моделью для пояснения принципа восстановления непрерывного сигнала на основе теоремы Котельникова. Реальный ФНЧ имеет частотную характеристику, которая либо охватывает несколько лепестков спектра (штрихпунктирная линия на рис. 9.9) либо имеет конечную крутизну ската характеристики и не полностью охватывает центральный лепесток. Этот недостаток накладывает определенные ограничения на применение теоремы Котельникова, требуя уменьшения интервала дискретизации непрерывных сигналов. На практике интервал дискретизации, определяемый формулой Котельникова, уменьшают в 2...5 раз. В этом случае отдельные составляющие спектра дискретного сигнала не перекрываются, как это и показано на рис. 9.9, и могут быть разделены фильтрами.

С уменьшением длительности дискретизирующего импульса τ_И амплитуды спектральных составляющих убывают медленнее. В предельном случае, при τ_И → 0 , спектр дискретного сигнала будет представлять собой бесконечную последовательность «копий» спектров исходного сигнала, имеющих равную амплитуду. Если одновременно с уменьшением длительности увеличивать амплитуду импульса так, чтобы его площадь оставалась неизменной и равной единице, то теоретически дискретизирующим сигналом может быть бесконечная последовательность дельта-функций:

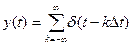
В этом случае формула запишется следующим образом:

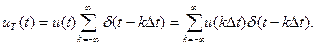(9.10)

Итак, согласно последнему выражению дискретный сигнал u_Т(t) при подобной дискретизации представляет собой последовательность дельта-функций, следующих с интервалом времени Δt. Эти функции имеют амплитудные коэффициенты, равные выборкам (уровням) аналогового сигнала u(t) в точках дискретизации t = k∆t.

Аналитическое выражение для спектральной плотности дискретного сигнала в этом случае имеет вид:

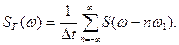(9.11)

Пример 9.3.

Непрерывный сигнал, имеющий форму прямоугольного импульса напряжения с единичной амплитудой и длительностью τ_И , дискретизирован 10 отчетами. Определить спектр дискретного сигнала.

Р е ш е н и е Для нахождения спектра можно воспользоваться формулой (9.11). В ней частота ω₁ = 2π/Δt = 20π/ τ_И, интервал дискретизации Δt= τ_И/10, а спектральная плотность дискретизируемого прямоугольного импульса определяется выражением (9.8). Тогда

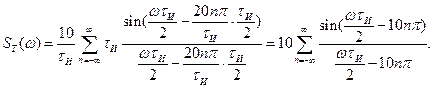
Возможность представления дискретных сигналов u_Т(t) в форме (9.10) существенно упрощает их анализ. В частности, спектральную плотность S_T(ω). можно вычислить непосредственно по совокупности временн'ых отсчетов {u(k∆t)}. Действительно, применив прямое преобразование Фурье (1.16) к соотношению (9.10) для отчетов только с положительными номерами

k = 0, 1..., ∞, получим с учетом фильтрующего свойства дельта-функции:

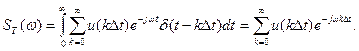(9.12)

При этом существенно сокращается время обработки реальных непрерывных сигналов.