ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ

Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение.

Механику подразделяют на:

§ классическую - рассматривает движение макроскопических тел, совершающиеся со скоростями, во много раз меньшими скорости света в вакууме. В основе классической механики лежат законы Ньютона. Поэтому её часто называют ньютоновской механикой;

§ релятивистскую - изучает закономерности движения тел со скоростями, близкими к скорости света в вакууме. В основе релятивистской механики лежит специальная теория относительности (СТО), сформулированная А. Эйнштейном;

§ квантовую – изучает закономерности движения микрочастиц (например, электронов в атомах, молекулах, кристаллах и т.п.)

Классическую механику (в дальнейшем будем просто говорить механика) подразделяют обычно на три основных раздела:

- кинематика - математически описывает, классифицирует по типам и исследует характерные особенности разных видов движения;

- динамика – выясняет причины, вызывающие движение, рассматривает вопрос о взаимодействии тел;

- статика – частный случай динамики. В статике рассматриваются законы сложения сил и условия равновесия тел.

Для описания реальных движущихся тел в механике пользуются различными упрощёнными моделями, такими как: материальная точка, система материальных точек, абсолютно твёрдое тело.

Материальная точка (м.т.) – тело, обладающее массой, размерами которого в условиях данной задачи можно пренебречь.

Система материальных точек – произвольное макроскопическое тело или система тел, мысленно разбитых на малые взаимодействующие между собой части, каждая из которых рассматривается как материальная точка.

Абсолютно твёрдое тело – тело, деформацией которого в условиях данной задачи можно пренебречь и при любых воздействиях расстояние между любыми двумя точками остаётся постоянным.

Движение тела – сложный процесс, поэтому мы будем рассматривать последовательно различные его стороны, а затем уже будем связывать их между собой и объединять в одно целое.

Чтобы ясно себе представить движение тела, достаточно иметь указания о движении или покое отдельных его точек.

Относительность движения и покоя. Можно ли сказать, что книга, лежащая на столике движущегося вагона, находится в покое? И, да и нет. Да – потому, что она не движется по вагону. Нет – потому, что она движется вместе с вагоном.

Можно сказать, что наша книга находится в покое относительно вагона, но движется относительно земли. А если эта книга лежит на журнальном столике в вашей квартире? Тогда она находится в покое относительно столика, дома, Земли, но движется относительно Солнца, так как сама Земля со всем, что на ней находится, вращается вокруг Солнца, пробегая каждую секунду около 30 км. Солнце вместе с движущимися вокруг него планетами само движется относительно звёзд. И звёзды в свою очередь движутся друг относительно друга, хотя мы и не замечаем этого благодаря их удалённости от нас. Обобщая всё это можно сказать, что в природе не существует тел, которые можно было бы назвать абсолютно неподвижными. Поэтому всякий покой относителен.

Относительно и всякое движение. Это значит, что одно и то же движение разные наблюдатели могут видеть по-разному и приписывать ему разные свойства в зависимости от того, откуда они наблюдают.

Простейшим видом движения в природе является механическое движение.

Механическое движение – это изменение взаимного расположения тел или их частей в пространстве с течением времени. Например, теплоходы движутся, изменяя своё положение относительно берегов рек, морей и океанов.

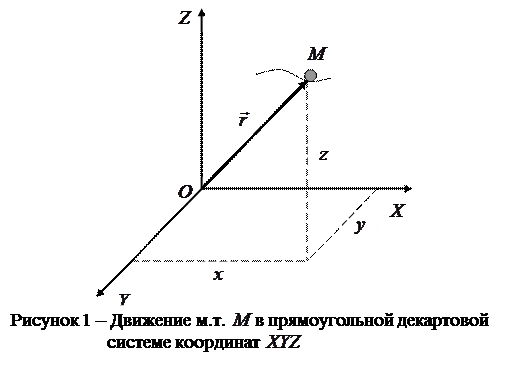
Для описания механического движения необходимо указать тело, относительно которого рассматривается движение – тело отсчёта (т.о.). С телом отсчёта связана система координат. Простейшей системой координат является прямоугольная декартова система (рис.1).

Совокупность тела отсчёта, системы координат и системы отсчёта времени, связанных с этим телом, по отношению к которому изучается движение (или равновесие) каких-либо других материальных точек или тел, называется системой отсчёта.

При движении материальной точки 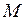(рис.1) конец радиус-вектора 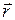описывает в пространстве некоторую линию.

Координаты материальной точки 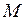при её движении с течением времени изменяются и описываются системой уравнений:

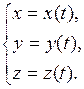(I.1)

Эта система эквивалентна векторному уравнению, называемому законом движения:

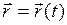. (I.2)

Уравнения (I.1) и (I.2) называются кинематическими уравнениями движения материальной точки.

Положение точки в пространстве определяется числом независимых координат, называемых числом степеней свободы.

Рассмотрим частные случаи:

§ три степени свободы ( 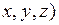- материальная точка свободно движется в пространстве;

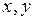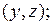
§ две степени свободы ( ); 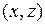- материальная точка движется по некоторой поверхности;

§ одна степень свободы 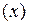, 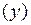или 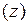- материальная точка движется вдоль некоторой линии.

Исключая время 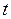в уравнениях (I.1) и (I.2), получим уравнение траектории движения материальной точки.

Траекторией движения материальной точки называется линия, которую описывает эта движущаяся точка в пространстве.

В зависимости от формы траектории мы будем называть движение точки прямолинейным или криволинейным. Например, движение выпущенного из рук камня – прямолинейное, а движение артиллерийского снаряда – криволинейное.

Простейшими видами механического движения являются поступательное и вращательное движения тела.

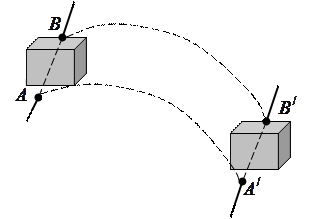
Поступательное движение – это движение, при котором любая прямая, соединяющая две произвольные точк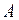и ( и 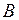) тела, перемещается, оставаясь параллельной самой себе (рис.2).

	Рисунок 2 – Поступательное движение тела

Например, поступательно движется ящик письменного стола, когда его выдвигают.

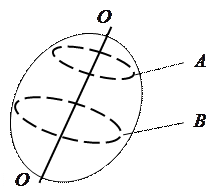Вращательное движение – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, перпендикулярной к плоскостям окружностей, называемой осью вращения (ОО) (рис.3).

	Рисунок 3 – Вращательное движение тела