I.1.6 СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
Падение тел происходит по законам равнопеременного движения; это было установлено Галилеем при движении шарика по наклонной плоскости и может быть продемонстрировано при помощи машины Атвуда и многих других приборов, которые имеют целью замедлить движение и сделать явление падения легко наблюдаемым.
Свободным падением называется движение, которое совершало бы тело только под действием силы тяжести без учёта сопротивления воздуха.
При свободном падении тела с небольшой высоты 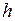 от поверхности Земли (
от поверхности Земли ( 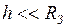 , где
, где 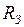 - радиус Земли) оно движется с постоянным ускорением
- радиус Земли) оно движется с постоянным ускорением 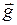 , направленным по вертикали вниз.
, направленным по вертикали вниз.
Ускорение 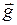 называется ускорением свободного падения. Оно одинаково для всех тел и зависит лишь от высоты над уровнем моря и от географической широты.
называется ускорением свободного падения. Оно одинаково для всех тел и зависит лишь от высоты над уровнем моря и от географической широты.
Величина нормального ускорения свободного падения (т.е. на уровне моря на 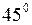 северной широты) составляет
северной широты) составляет 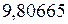 м/с2. На полюсах ускорение свободного падения больше (
м/с2. На полюсах ускорение свободного падения больше ( 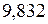 м/с2), а на экваторе меньше (
м/с2), а на экваторе меньше ( 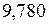 м/с2). Это обусловлено суточным вращением Земли вокруг своей оси, с одной стороны, и сплюснутостью Земли – с другой (экваториальный и полярный радиусы Земли равны соответственно 6378 и 6357 км). Различие значений
м/с2). Это обусловлено суточным вращением Земли вокруг своей оси, с одной стороны, и сплюснутостью Земли – с другой (экваториальный и полярный радиусы Земли равны соответственно 6378 и 6357 км). Различие значений 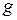 невелико, поэтому ускорение свободного падения, которое используется при решении практических задач, принимается равным 9,81 м/с2.
невелико, поэтому ускорение свободного падения, которое используется при решении практических задач, принимается равным 9,81 м/с2.
Законы движения падающего тела, вследствие постоянства 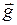 (в скалярном виде), имеют вид:
(в скалярном виде), имеют вид:
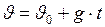 ; (I.21)
; (I.21)
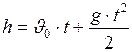 , (I.22)
, (I.22)
где 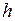 - путь, пройденный телом в свободном падении, к моменту времени
- путь, пройденный телом в свободном падении, к моменту времени 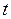 .
.
Применим их к некоторым частным случаям.
1. Свободное падение с высоты 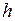 . Свободное падение представляет собой частный случай равноускоренного движения при
. Свободное падение представляет собой частный случай равноускоренного движения при 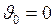 :
:
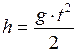 ;
; 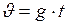 . (I.23)
. (I.23)
Скорость, с которой падающее тело достигает поверхности Земли, определяется по формуле:
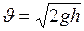 . (I.24)
. (I.24)
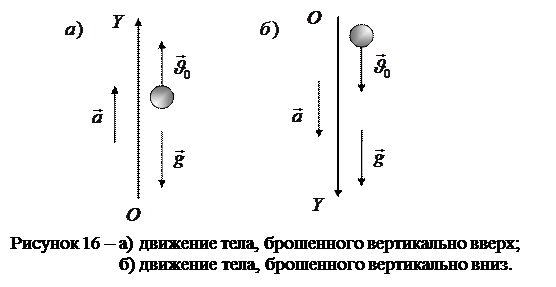
2. Движение тела, брошенного вертикально вверх (рис.16,а). Тело, брошенное вертикально вверх, движется равнозамедленно с начальной скоростью 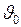 и ускорением
и ускорением 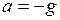 . Для описания этого движения, используют следующие формулы:
. Для описания этого движения, используют следующие формулы:
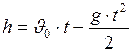 . (I.25)
. (I.25)
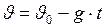 . (I.26)
. (I.26)
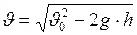 . (I.27)
. (I.27)
Движение тела, брошенного вертикально вниз (рис.16,б), представляет собой равноускоренное движение с ускорением 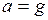 . Для его описания можно воспользоваться формулами (I.25) - (I.27), поменяв в них знак «-» на «+».
. Для его описания можно воспользоваться формулами (I.25) - (I.27), поменяв в них знак «-» на «+».
Тело, брошенное вертикально вверх, достигает максимальной высоты в тот момент, когда его скорость обращается в нуль:
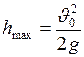 . (I.28)
. (I.28)
А из формулы (I.26) найдём время подъёма тела на максимальную высоту:
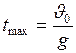 . (I.29)
. (I.29)
 |
3. Движение тела, брошенного горизонтально. Движение тела, брошенного горизонтально, представляет собой комбинацию двух движений, взаимно перпендикулярных друг другу:
q горизонтального (равномерного) движения;
q вертикального (свободного падения).
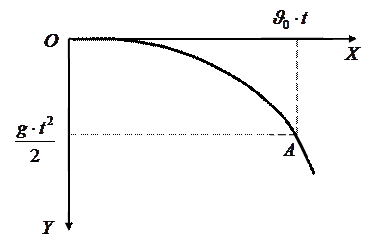
Если построить траекторию движения тела, брошенного горизонтально, в системе координат 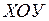 , то координаты каждой точки
, то координаты каждой точки 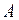 траектории представляют собой перемещения тела в горизонтальном направлении (движение с постоянной скоростью
траектории представляют собой перемещения тела в горизонтальном направлении (движение с постоянной скоростью 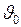 ) и в вертикальном направлении (равноускоренное движение с ускорением
) и в вертикальном направлении (равноускоренное движение с ускорением 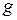 ) (рис.16, в):
) (рис.16, в):
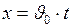 ;
; 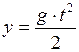 . (I.30)
. (I.30)
 | |||
|
Подставив 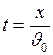 во второе уравнение (I.30), получим уравнение траектории тела, брошенного горизонтально:
во второе уравнение (I.30), получим уравнение траектории тела, брошенного горизонтально:
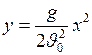 . (I.31)
. (I.31)
Так как 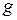 и
и 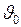 - постоянные величины, то
- постоянные величины, то 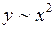 , т.е. траектория движения представляет собой параболу.
, т.е. траектория движения представляет собой параболу.
 | |||
|
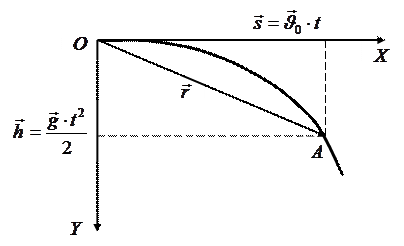
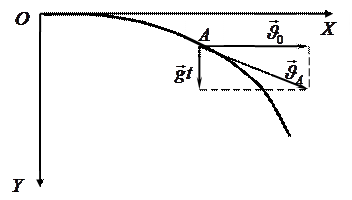
Положение каждой точки траектории можно задать вектором положения 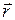 (рис.17), который представляет собой результирующее перемещение:
(рис.17), который представляет собой результирующее перемещение: 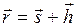 , или
, или
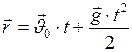 (I.32)
(I.32)
 | |||
|
Вектор мгновенной скорости 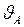 в каждой точке траектории является результирующей мгновенных скоростей этих движений (рис.18):
в каждой точке траектории является результирующей мгновенных скоростей этих движений (рис.18):
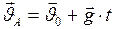 . (I.33)
. (I.33)
Модуль вектора (I.33) запишется как:
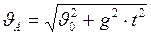 . (I.34)
. (I.34)
4. Движение тела, брошенного под углом к горизонту. Движение тела, брошенного под углом к горизонту, представляет собой комбинацию двух поступательных движений:
q свободного падения в вертикальном направлении;
q равномерного прямолинейного движения под углом 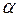 к горизонту.
к горизонту.
 | |||
|
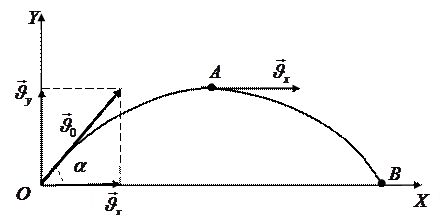
На рисунке 19 представлена траектория движения тела, брошенного под углом к горизонту.
Перемещение тела к моменту времени 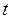 в горизонтальном и вертикальном направлениях будет определяться следующим образом:
в горизонтальном и вертикальном направлениях будет определяться следующим образом:
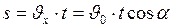 , (I.35)
, (I.35)
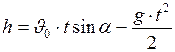 . (I.36)
. (I.36)
В наивысшей точке 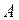 подъёма:
подъёма: 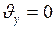 . Тогда уравнение (I.26) для скорости будет иметь вид:
. Тогда уравнение (I.26) для скорости будет иметь вид: 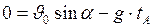 , где
, где 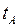 -время подъёма на максимальную величину:
-время подъёма на максимальную величину:
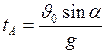 . (I.37)
. (I.37)
Для нахождения общего времени движения, рассмотрим точку 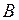 . В этой точке:
. В этой точке: 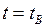 ;
; 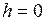 . Тогда уравнение (I.25), перепишется в виде:
. Тогда уравнение (I.25), перепишется в виде:
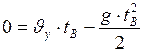 , где
, где 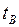 - общее время движения. Выразим его:
- общее время движения. Выразим его:
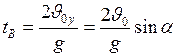 . (I.38)
. (I.38)
Максимальная высота подъёма определится по формуле:
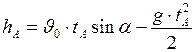 . Подставим сюда выражение (I.37), получим:
. Подставим сюда выражение (I.37), получим:
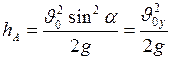 . (I.39)
. (I.39)
Дальность броска определяется по формуле (I.35):
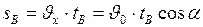 . Подставив выражение (I.38), получим:
. Подставив выражение (I.38), получим:
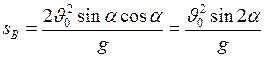 . (I.40)
. (I.40)
На что необходимо обратить внимание:
q Сопротивление воздуха не учитывалось.
q При постоянной начальной скорости дальность броска зависит от угла.
Из формулы (I.40) следует, что она максимальна при 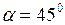 , так как
, так как 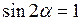 . При значениях
. При значениях 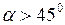 и
и 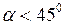 дальность броска будет меньше.
дальность броска будет меньше.
Дата добавления: 2016-09-06; просмотров: 3386;











