I.1.7 ДВИЖЕНИЕ ТЕЛА ПО ОКРУЖНОСТИ

Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения.

Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних небольшие замены (см. таблицу 2).

Таблица 2

движение
поступательное	вращательное
равномерное
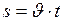
линейное перемещение	угловое перемещение (угол поворота)
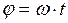
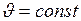
линейная скорость	угловая скорость
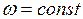
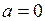
линейное ускорение	угловое ускорение
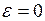
равнопеременное
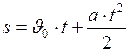
линейное перемещение	угловое перемещение
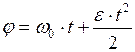
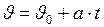
линейная скорость	угловая скорость
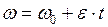
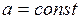
линейное ускорение	угловое ускорение
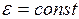
неравномерное
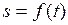
линейное перемещение	угловое перемещение
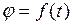
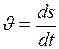
линейная скорость	угловая скорость
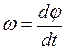
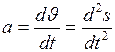
линейное ускорение	угловое ускорение

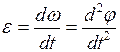
Связь между линейными и угловыми величинами:

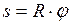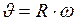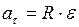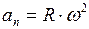; ; ; . (I.41)

Характеристикой всех видов вращения является число оборотов 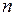или равноценная ей характеристика – частота 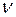. Обе величины характеризуют число оборотов в единицу времени.

Величина, обратная числу оборотов, есть продолжительность одного оборота.

Частота вращения – число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени.

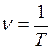, (I.42)

где 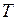- период вращения.

Период вращения 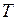- время, за которое точка совершает один полный оборот, т.е. поворачивается на угол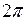

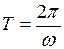. (I.43)

Мерой перемещения всего тела за малый промежуток времени 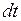служит вектор 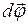элементарного поворота тела. По модулю он равен углу 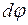поворота тела вокруг оси за время 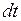и направлен вдоль оси вращения по правилу правого винта: из конца вектора 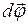поворот тела виден происходящим против хода часовой стрелки.

Угловой скоростью 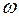называется векторная величина, равная первой производной угла поворота тела по времени:

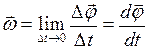. (I.44)

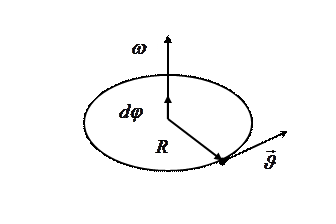Вектор 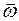направлен вдоль оси вращения по правилу правого винта, т.е. так же, как и вектор 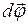(рис.20).

	Рисунок 20 – Определение направления вектора угловой скорости

Если 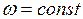, то вращение равномерное, т.е. тело за равные промежутки времени поворачивается на один и тот же угол

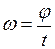. (I.45)

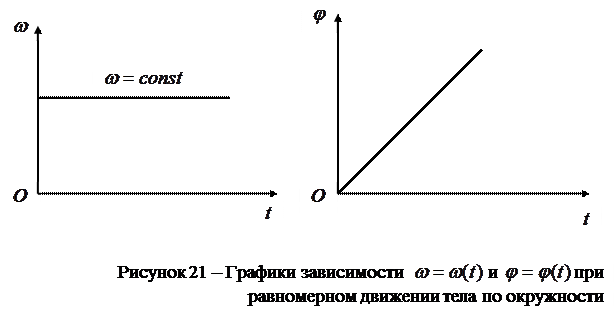
При равномерном движении тела по окружности, графики зависимости углового перемещения и угловой скорости от времени имеют вид (рис.21):

Угловым ускорением 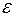называется векторная величина, равная первой производной угловой скорости по времени:

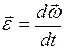. (I.46)

При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор 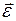сонаправлен вектору 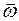(рис.22,а), при замедленном – противоположно направлен ему (рис.22,б).

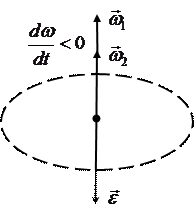
а) б)

	Рисунок 22 – Направления векторов и при: а) ускоренном; б)замедленном движении тела

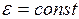Если и 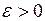, то движение тела по окружности называется равноускоренным.

При равноускоренном движении тела по окружности, графики зависимости углового перемещения (рис.23,б) и угловой скорости от времени (рис.23,а) имеют вид:

а) б)

	Рисунок 23 - Графики зависимости а) и б) для равноускоренного движения тела по окружности

При равнопеременном вращательном движении мгновенное ускорение тела остаётся неизменным и совпадает со средним угловым ускорением: .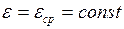

В этом случае угловое ускорение будет равно отношению изменения угловой скорости к продолжительности этого изменения:

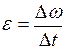. (I.47)

Угловое ускорение на графике зависимости угловой скорости от времени (рис.23,а), характеризуется тангенсом угла между касательной к кривой скорости и осью времени: .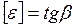

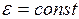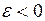Если и , то движение тела по окружности называется равнозамедленным.

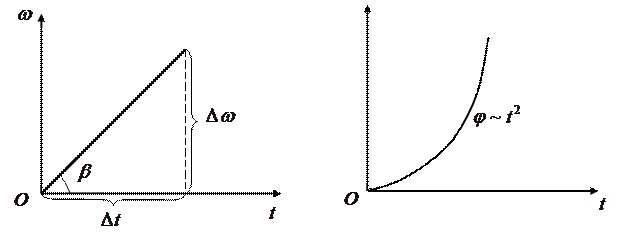
При равнозамедленном движении тела по окружности, графики зависимости углового перемещения (рис.24,б) и угловой скорости от времени (рис.24,а) имеют вид:

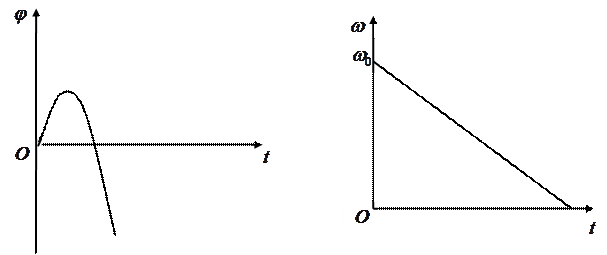а) б)

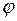
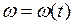	Рисунок 24 - Графики зависимости а) и б) 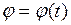для равнозамедленного движения тела по окружности