I.1.3 СКОРОСТЬ. УСКОРЕНИЕ.
Для характеристики быстроты движения тел в механике вводится понятие скорости.
Различают: среднюю и мгновенную скорости.
Средней скоростью за промежуток времени  называется физическая величина, равная отношению приращения
называется физическая величина, равная отношению приращения 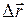 радиус-вектора материальной точки к промежутку времени
радиус-вектора материальной точки к промежутку времени  :
:
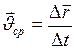 . (I.3)
. (I.3)
Средняя скорость характеризует движение в течение всего того промежутка времени, для которого она определена.
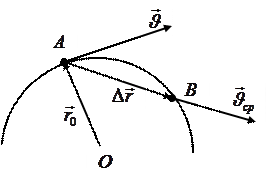
Направление вектора средней скорости совпадает с направлением приращения радиус-вектора, т.е. направлен вдоль хорды, стягивающей соответствующий участок траектории точки (рис. 4 и 6).
Мгновенной скоростью (скоростью), называется физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени  :
:
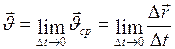 . (I.4)
. (I.4)
Мгновенная скорость является первой производной по времени от радиус-вектора рассматриваемой точки:
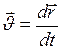 . (I.5)
. (I.5)
Вектор мгновенной скорости материальной точки направлен по касательной к траектории в сторону движения (рис. 6).
 | |||
|
Для характеристики быстроты изменения скорости точки в механике вводится понятие ускорения.
Средним ускорением называется физическая величина, равная отношению изменения скорости материальной точки к длительности промежутка времени  , в течение которого это изменение произошло:
, в течение которого это изменение произошло:
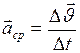 . (I.6)
. (I.6)
Направление векторов 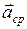 и
и 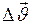 совпадают (рис.7).
совпадают (рис.7).
 | |||
|
Мгновенным ускорением (ускорением) материальной точки в момент времени 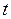 называется физическая величина, равная пределу, к которому стремится среднее ускорение при бесконечном уменьшении промежутка времени
называется физическая величина, равная пределу, к которому стремится среднее ускорение при бесконечном уменьшении промежутка времени  :
:
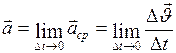
 . (I.7)
. (I.7)
Мгновенное ускорение является первой производной по времени скорости рассматриваемой точки, или второй производной по времени от радиус-вектора этой точки:
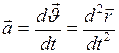 . (I.8)
. (I.8)
Вектор ускорения точки можно разложить на две составляющие: тангенциальную 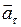 и нормальную
и нормальную 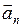 .
.
Тангенциальная составляющая вектора ускорения направлена вдоль касательной к траектории в данной точке и называется тангенциальным (касательным) ускорением:
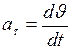 . (I.9)
. (I.9)
Тангенциальное ускорение характеризует изменение вектора скорости по модулю. Вектор 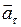 направлен в сторону движения точки при возрастании её скорости и в противоположную сторону – при убывании скорости.
направлен в сторону движения точки при возрастании её скорости и в противоположную сторону – при убывании скорости.
Нормальная составляющая вектора ускорения, направлена по нормали к траектории к центру её кривизны в данной точке и называется нормальным (центростремительным) ускорением:
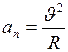 . (1.10)
. (1.10)
Нормальное ускорение характеризует изменение вектора скорости по направлению при криволинейном движении.
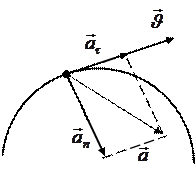
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис.8):
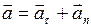 . (I.11)
. (I.11)
 | |||
|
В зависимости от тангенциальной и нормальной составляющих ускорения, движение будет подразделяться на несколько видов (таблица 1.):
Таблица 1. Классификация движения в зависимости от составляющих ускорения: тангенциального ( 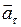 ) и нормального (
) и нормального ( 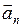 ).
).
| N | 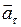
| 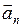
| Вид движения |
| равномерное прямолинейное | |||
| const | равнопеременное прямолинейное | ||
| f(t) | прямолинейное движение с переменным ускорением | ||
| const | равномерное движение по окружности | ||
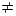 0 0
| равномерное криволинейное движение | ||
| const | 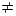 0 0
| равнопеременное криволинейное движение | |
| f(t) | 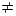 0 0
| криволинейное движение с переменным ускорением |
Дата добавления: 2016-09-06; просмотров: 3529;











