A. Яблонский А.А. Курс теоретической механики. Ч. 2, «Высшая школа», С-Птб.: 2002 и предшествующие издания.
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Ч.1 и 2. М., 1961 и последующие издания
Контрольные задания для СРС – рассмотреть и решить следующую задачу самостоятельно: груз массой 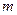 движется по наклонной плоскости с углом наклона
движется по наклонной плоскости с углом наклона 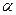 ; коэффициент трения груза о плоскость равен
; коэффициент трения груза о плоскость равен 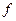 . Одинаковы ли дифференциальные уравнения движения груза по этой плоскости вниз и вверх?
. Одинаковы ли дифференциальные уравнения движения груза по этой плоскости вниз и вверх?
Лекция 10. Введение в динамику системы. Геометрия масс.
Цель лекции – изложить основные понятия динамики механической системы, дать основные понятия геометрии масс.
План лекции
Механическая система. Внешние и внутренние силы
Масса системы. Центр масс механической системы
Моменты инерции. Теорема Штейнера-Гюйгенса
КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ
Любая совокупность материальных точек называется механической системой.
Все силы, действующие на элементы данной механической системы, разделяют на внутренние и внешние. Силы ( 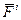 ) взаимодействия точек данной системы называют внутренними. Силы (
) взаимодействия точек данной системы называют внутренними. Силы ( 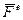 ), действующие на механическую систему со стороны точек (тел), не входящих в состав данной системы, называют внешними. Заметим, что к внешним силам будут относиться и реакции связей. В соответствии с первой аксиомой динамики любые две точки системы действуют друг на друга с силами, равными по величине и противоположными по направлению. Отсюда следуют два свойства внутренних сил: 1) геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю, т.е.
), действующие на механическую систему со стороны точек (тел), не входящих в состав данной системы, называют внешними. Заметим, что к внешним силам будут относиться и реакции связей. В соответствии с первой аксиомой динамики любые две точки системы действуют друг на друга с силами, равными по величине и противоположными по направлению. Отсюда следуют два свойства внутренних сил: 1) геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю, т.е. 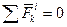 ; 2) сумма моментов (главный момент) всех внутренних сил системы относительно любого центра (оси) равняется нулю, т.е.
; 2) сумма моментов (главный момент) всех внутренних сил системы относительно любого центра (оси) равняется нулю, т.е. 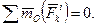
Под действием внутренних сил могут возникать взаимные перемещения точек (или тел) механической системы. Система, расстояния между любыми двумя точками которой остаются при движении постоянными, называется неизменяемой. Если расстояние между какими-либо двумя точками системы изменяется при движении, то систему называют изменяемой. Масса и взаиморасположение масс системы являются существенными факторами, влияющими на ее движение. Эти характеристики системы отражаются соответствующими величинами.
Механическая система – это система материальных точек, каждая из которых имеет определенную массу и занимает в данный момент времени определенное положение в пространстве. Рассмотрим систему, состоящую из п материальных точек. Распределение масс в системе можно определить значениями масс 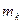 ее точек и их координатами
ее точек и их координатами 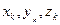 . Масса системы М равна арифметической сумме масс всех точек или тел, образующих систему. Если система представляет собой твердое тело, то его масса является мерой инертности тела при поступательном движении.
. Масса системы М равна арифметической сумме масс всех точек или тел, образующих систему. Если система представляет собой твердое тело, то его масса является мерой инертности тела при поступательном движении.
Центром масс механической системы называют геометрическую точку С, радиус- вектор которой определяется по формуле:
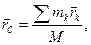 (*)
(*)
где 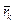 - радиус-векторы точек, образующих систему.
- радиус-векторы точек, образующих систему.
При непрерывном распределении массы системы сумма, стоящая в правой части формулы, переходит в соответствующий интеграл. В однородном поле силы тяжести вес любой частицы тела пропорционален ее массе и центр масс любой системы совпадает с ее центром тяжести. В динамике следует говорить о центре масс механической системы, а не о центре тяжести. Векторная величина, стоящая в числителе выражения (*) называется статическим моментом массы системы относительно точки О.
При исследовании движения системы недостаточно знать ее массу и положение центра масс. Необходимо также определять и другие характеристики распределения масс, которые называются моментами инерции.
Моментом инерции механической системы относительно центра (полярным моментом) называется сумма произведений масс всех точек системы на квадраты их расстояний до центра
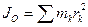 .
.
Моментом инерции относительно оси называется скалярная величина, равная сумме произведений масс всех точек системы на квадраты их расстояний до этой оси
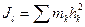 .
.
Из определений следует, что момент инерции системы (тела) является величиной положительной, не равной нулю.
Осевой момент инерции тела является мерой инертности тела при его вращательном движении.
Моменты инерции данного тела относительно разных осей будут иметь разные значения. Зависимость между моментами инерции системы относительно двух параллельных осей, одна из которых проходит через центр масс системы, определяется по теореме Штейнера-Гюйгенса. Согласно этой теореме, момент инерции системы относительно какой либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс системы, сложенному с произведением массы системы на квадрат расстояния между этими осями, т.е.
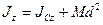 .
.
Из этой формулы видно, что при удалении оси 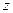 от оси
от оси 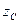 величина момента инерции
величина момента инерции 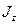 возрастает.
возрастает.
ГЛОССАРИЙ
| Механикалық жүйе | Механическая система | System |
| Механикалық жүйенiң массалар центрi | Центр масс механической системы | Center of mass |
| Механикалық жүйенiң нүктеге, өске қатысты инерция моментi | Момент инерции механической системы относительно точки (центра) | Moment of inertia of system about point, axis |
Рекомендуемая литература
Дата добавления: 2016-07-22; просмотров: 2985;











