I.1.2 ВЕКТОР ПЕРЕМЕЩЕНИЯ. ПУТЬ
При движении точки положение её радиус-вектора в пространстве изменяется. Приращение радиус-вектора, характеризующего конечное и начальное положения точки, движущейся в течение некоторого промежутка времени  , называется вектором перемещения (перемещением)
, называется вектором перемещения (перемещением) 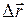 (
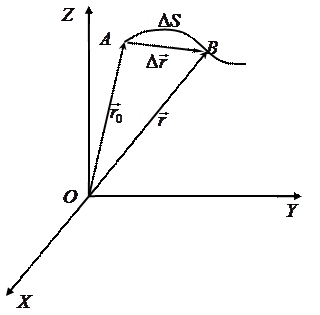
( 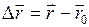 ). Вектор перемещения направлен вдоль хорды траектории точки (рис.4).
). Вектор перемещения направлен вдоль хорды траектории точки (рис.4).
 | |||
|
Векторы перемещений складываются геометрически, по правилу параллелограмма или многоугольника (правило сложения векторов) (см. приложение 1).
Путь ( 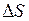 или
или  ) (рис.4) - скалярная величина (скалярная функция времени:
) (рис.4) - скалярная величина (скалярная функция времени: 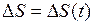 ), равная длине участка траектории, пройденного движущейся точкой за данный промежуток времени. Пути, пройденные точкой за последовательные промежутки времени, складываются алгебраически.
), равная длине участка траектории, пройденного движущейся точкой за данный промежуток времени. Пути, пройденные точкой за последовательные промежутки времени, складываются алгебраически.
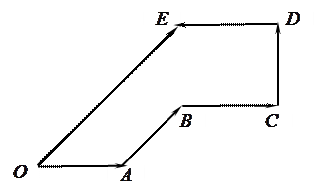
Пример: Материальная точка последовательно перемещается из положения 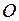 в положение
в положение 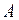 , затем в
, затем в 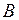 ,
,  и т.д. (рис. 5).
и т.д. (рис. 5).
 | |||
|
Путь, пройденный материальной точкой, будет равен сумме длин участков траектории:
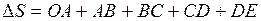 .
.
Вектор перемещения 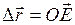 соединяет начальное положение точки с её конечным положением. В рассмотренном примере модуль вектора перемещения
соединяет начальное положение точки с её конечным положением. В рассмотренном примере модуль вектора перемещения 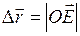 не равен пути
не равен пути 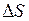 , пройденному материальной точкой.
, пройденному материальной точкой.
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения 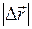 равен пройденному пути
равен пройденному пути 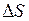 .
.
Дата добавления: 2016-09-06; просмотров: 3743;











