Законы Кирхгофа в матричной форме
Для записи законов Кирхгофа в матричной форме необходимо составить топологические графы и топологические матрицы схемы.
Допустим, имеется электрическая цепь, приведенная на рисунке 2.9.
Представленная электрическая цепь, состоит из шести ветвей  (1 - 2, 1- 4, 1 - 3, 4 - 2, 3 - 4, 2 - 3), четырех узлов
(1 - 2, 1- 4, 1 - 3, 4 - 2, 3 - 4, 2 - 3), четырех узлов  (1, 2, 3, 4) и трех главных сечений S1, S2, S3. Граф схемы представлен на рисунке 2.10.
(1, 2, 3, 4) и трех главных сечений S1, S2, S3. Граф схемы представлен на рисунке 2.10.
Ветвями дерева приняты ветви 2,5,4. Ветви связи (1,3,6) обозначены на схеме пунктирными линиями.
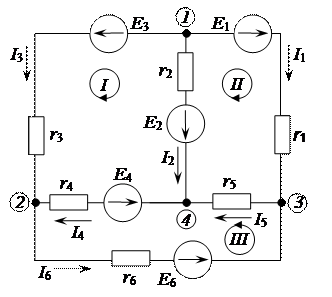
Рисунок 2.9 – Электрическая цепь постоянного тока
Матрица соединений (узловая матрица) Апредставляет собой таблицу коэффициентов независимых уравнений, составленных по первому закону Кирхгофа для  узлов. Строки i матрицы соответствуют узлам (их число равно
узлов. Строки i матрицы соответствуют узлам (их число равно 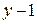 ), столбцы j – ветвям (их число равно в). Элемент матрицы
), столбцы j – ветвям (их число равно в). Элемент матрицы 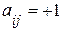 , если ветвь j графа соединена с узлом i и направлена от данного узла. Элемент матрицы
, если ветвь j графа соединена с узлом i и направлена от данного узла. Элемент матрицы 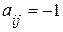 , если ветвь j графа соединена с узлом i и направлена к данному узлу. Элемент матрицы
, если ветвь j графа соединена с узлом i и направлена к данному узлу. Элемент матрицы 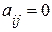 , если ветвь j не присоединена к узлу i.
, если ветвь j не присоединена к узлу i.
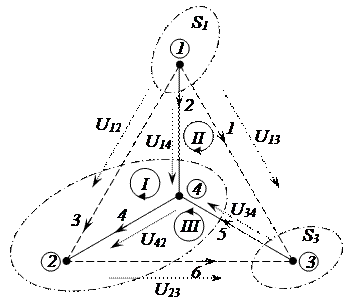
Рисунок 2.10 – Граф исходной схемы
Например, для электрической цепи, приведенной на рисунке 2.9 и ее графа (рис. 2.10), матрица соединений для первых трех узлов будет иметь вид
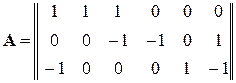 .
.
Так как матрица определяет, какие ветви присоединены к каждому узлу и как направлены токи в этих ветвях, то произведение матрицы соединении на матрицу-столбец токов ветвей 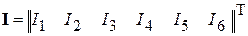 дает совокупность левых частей уравнений, составленных по первому закону Кирхгофа, и, следовательно, равна нулю. Т.е., первый закон Кирхгофа в матричной форме имеет вид
дает совокупность левых частей уравнений, составленных по первому закону Кирхгофа, и, следовательно, равна нулю. Т.е., первый закон Кирхгофа в матричной форме имеет вид 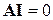 .
.
Под сечением 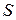 понимают любую замкнутую поверхность, рассекающую схему электрической цепи на две части: внешнюю по отношению к поверхности и внутреннюю. Его изображают в виде следа замкнутой поверхности, охватывающей часть схемы, включающей один или несколько узлов.
понимают любую замкнутую поверхность, рассекающую схему электрической цепи на две части: внешнюю по отношению к поверхности и внутреннюю. Его изображают в виде следа замкнутой поверхности, охватывающей часть схемы, включающей один или несколько узлов.
Например, для графа электрической цепи, приведенного на рисунке 2.10, сечение 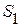 охватывает первую, вторую и третью ветви и узел 1; сечение
охватывает первую, вторую и третью ветви и узел 1; сечение 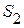 охватывает вторую, третью, пятую и шестую ветви и узлы 2 и 4; сечение
охватывает вторую, третью, пятую и шестую ветви и узлы 2 и 4; сечение 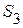 охватывает первую, пятую и шестую ветви и узел 3.
охватывает первую, пятую и шестую ветви и узел 3.
Матрица сечений Q– это таблица коэффициентов, составленных аналогично матрице соединений А. Строки i матрицы соответствуют сечениям (их число равно 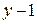 ), столбцы j – ветвям. Элемент матрицы
), столбцы j – ветвям. Элемент матрицы 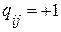 , если ветвь j содержится в сечении i и направлена согласно с направлением сечения. Элемент матрицы
, если ветвь j содержится в сечении i и направлена согласно с направлением сечения. Элемент матрицы 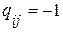 , если ветвь j содержится в сечении i и направлена противоположно направлению сечения. Элемент матрицы
, если ветвь j содержится в сечении i и направлена противоположно направлению сечения. Элемент матрицы 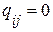 , если ветвь j не содержится в сечении i.
, если ветвь j не содержится в сечении i.
Например, для графа электрической цепи, приведенного на рисунке 2.10, при показанных трех главных сечений, матрица сечений имеет вид
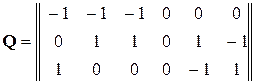 .
.
В матричной форме первый закон Кирхгофа, с использованием матрицы сечений, имеет вид 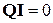 .
.
Матрица контуров В, представляет собой таблицу коэффициентов независимых уравнений, составленных по второму закону Кирхгофа для 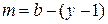 независимых контуров. Строки
независимых контуров. Строки 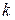 соответствуют контурам (их число равно
соответствуют контурам (их число равно 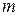 ), столбцы
), столбцы 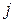 - ветвям. Элемент матрицы
- ветвям. Элемент матрицы 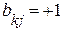 , если ветвь
, если ветвь 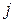 входит в состав контура
входит в состав контура 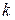 и ее направление совпадает с направлением обхода контура. Элемент матрицы
и ее направление совпадает с направлением обхода контура. Элемент матрицы 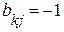 , если ветвь
, если ветвь 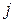 входит в состав контура
входит в состав контура 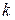 и ее направление противоположно направлению обхода контура. Элемент матрицы
и ее направление противоположно направлению обхода контура. Элемент матрицы 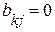 , если ветвь
, если ветвь 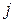 не входит в состав контура
не входит в состав контура 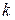 .
.
Матрица В, составленная для главных контуров, приводит непосредственно к независимой системе уравнений по второму закону Кирхгофа. Например, для графа, изображенного на рисунке 2.10, с контурами, состоящими из ветвей 2-4-3, 5-6-4 и 1-6-3 матрица главных контуров при обходе по направлению движения часовой стрелки
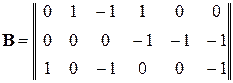 .
.
Умножив матрицуВна матрицу столбец напряжений ветвей, получим матричное уравнение по второму закону Кирхгофа 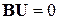 .
.
Для схемы (рис.2.9) и ее графа (рис.2.10) после умножения на матрицу-столбец напряжений 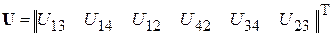 получим систему трех независимых уравнений вида:
получим систему трех независимых уравнений вида:
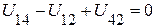 ;
;
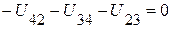 ;
;
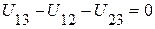 .
.
Если схема цепи кроме источников напряжения, содержит и источники тока, то для записи матричных уравнений, рекомендуется преобразование источников тока в источники напряжения.
Пример 2.4. По заданной матрице соединений А восстановить граф схемы. По заданным параметрам ветвей восстановить вид схемы и получить матрицу В. При помощи полученных матриц и параметров ветвей рассчитать токи в ветвях цепи. Составить баланс мощностей.
Матрица соединений
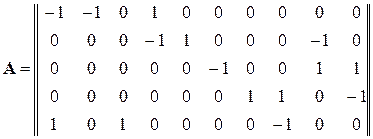 .
.
Параметры ветвей Е1 = 110 В, Е3 = 130 В, Е5 = 150 В, Е7 = 130 В, Е9 = 90 В, r1 = 10 Ом, r2 = 20 Ом, r3 = 12 Ом, r4 = 14 Ом, r5 = 20 Ом, r6 = 20 Ом, r7 = 15 Ом, r8 = 12 Ом, r9 = 16 Ом, r10 = 18 Ом.
1. Осуществляем предварительный анализ матрицы соединений.
1.1. Количество ветвей – 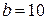 , количество узлов –
, количество узлов – 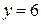 .
.
1.2. Вычерчиваем граф схемы, в котором выделяем ветви дерева и ветви связи.
Для данной матрицы соединени граф имеет вид, представленный на рисунке 2.11.
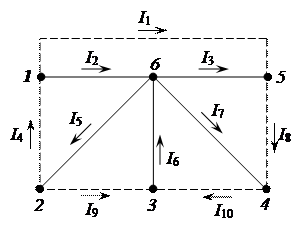
Рисунок 2.11 – Граф схемы
1.3. По приведенному графу составляем расчетную схему (направление токов в ветвях совпадает с направлением источников напряжениия). Электрическая схема с параметрами цепи и при данном графе, приведена на рисунке 2.12.
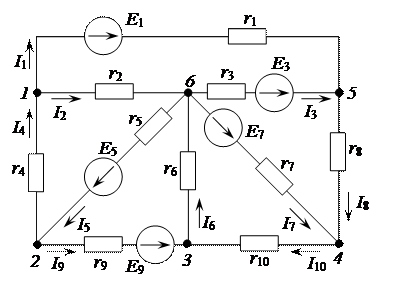
Рисунок 2.12 – Электрическая цепь
1.4. По приведенному на рисунке 2.13 графу, составленному при условии, что напряжения на зажимах каждой из ветвей, совпадает с направлением токов в этих ветвях, восстанавливаем матрицу контуров В.
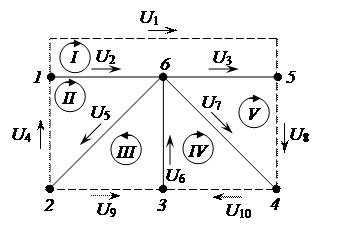
Рисунок 2.13 – Граф электрической цепи
Для приведенного графа, матрица контуров В имеет вид
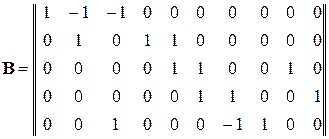 .
.
2. Составляем уравнения по законам Кирхгофа.
2.2. По первому закону Кирхгофа.
Произведение матрицы соединении А на матрицу-столбец токов ветвей 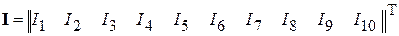 , дает совокупность левых частей уравнений, составленных по первому закону Кирхгофа
, дает совокупность левых частей уравнений, составленных по первому закону Кирхгофа
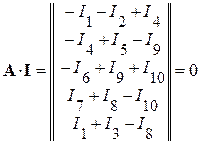 .
.
Таким образом,
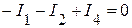 (1 узел);
(1 узел);
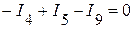 (2 узел);
(2 узел);
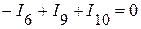 (3 узел);
(3 узел);
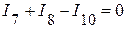 (4 узел);
(4 узел);
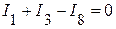 (5 узел).
(5 узел).
2.2. По второму закону Кирхгофа.
Произведение матрицы контуров В на матрицу-столбец напряжений ветвей 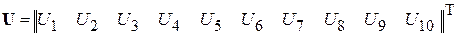 , дает совокупность левых частей уравнений, составленных по второму закону Кирхгофа
, дает совокупность левых частей уравнений, составленных по второму закону Кирхгофа
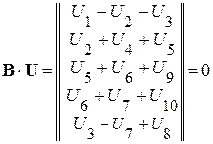 .
.
Таким образом,
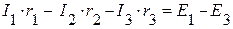 (I контур);
(I контур);
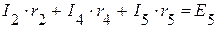 (II контур);
(II контур);
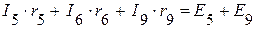 (III контур);
(III контур);
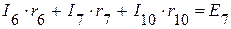 (IV контур);
(IV контур);
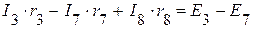 (V контур).
(V контур).
3. Подставляем числовые значения в полученную систему уравнений:
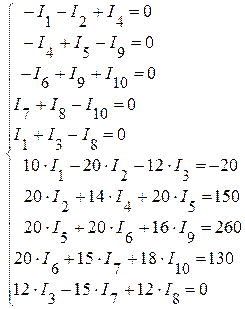
Решая данную систему уравнений, определяем токи в ветвях:
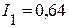 А,
А, 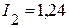 А,
А, 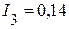 А,
А, 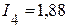 А,
А, 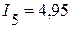 А,
А,
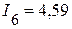 А,
А, 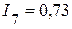 А,
А, 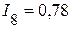 А,
А, 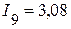 А,
А, 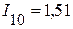 А.
А.
4. Проверяем решение системы уравнений, составив баланс мощностей.
4.1. Мощность источников:
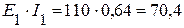 Вт,
Вт,
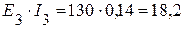 Вт,
Вт,
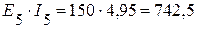 Вт,
Вт,
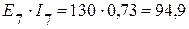 Вт,
Вт,
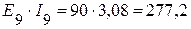 Вт.
Вт.
Суммарная мощность источников:
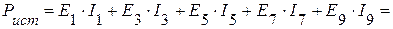
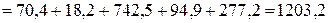 Вт.
Вт.
4.2. Мощность приемников:
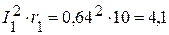 Вт,
Вт,
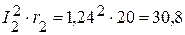 Вт,
Вт,
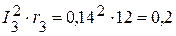 Вт,
Вт,
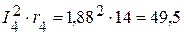 Вт,
Вт,
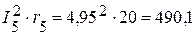 Вт,
Вт,
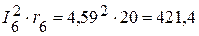 Вт,
Вт,
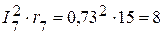 Вт,
Вт,
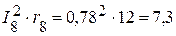 Вт,
Вт,
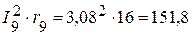 Вт,
Вт,
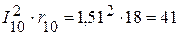 Вт.
Вт.
Суммарная мощность приемников:
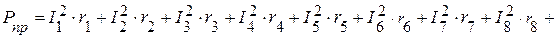
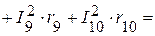
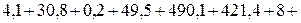
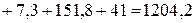 Вт.
Вт.
4.3. Из сравнения генерируемой мощности источниками и потребляемой мощности приемниками, следует, что погрешность вычислений 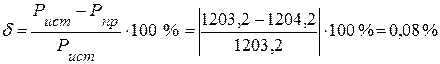 и не превышает 0,5%.
и не превышает 0,5%.
Пример 2.5. По заданной матрице контуров В восстановить граф схемы. По заданным параметрам ветвей восстановить вид схемы и получить матрицу соединений А. При помощи полученных матриц и параметров ветвей рассчитать токи в ветвях цепи. Составить баланс мощностей.
Матрица контуров
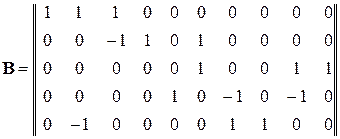 .
.
Параметры ветвей Е1 = 100 В, Е2 = 50 В, Е6 = 90 В, Е8 = 65 В, Е10 = 90 В, r1 = 10 Ом, r2 = 15 Ом, r3 = 12 Ом, r4 = 12 Ом, r5 = 20 Ом, r6 = 9 Ом, r7 = 8 Ом, r8 = 12 Ом, r9 = 16 Ом, r10 = 12 Ом.
1. Осуществляем предварительный анализ матрицы контуров.
1.1. Количество ветвей – 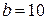 , количество контуров –
, количество контуров – 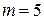 . Количесвтво узлов
. Количесвтво узлов 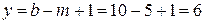
1.2. Вычерчиваем граф схемы, в котором выделяем ветви дерева и ветви связи.
Для данной матрицы соединени граф имеет вид, представленный на рисунке 2.14.
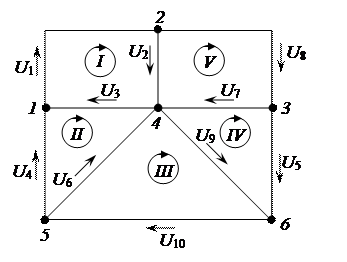
Рисунок 2.14 – Граф схемы
1.3. По приведенному графу составляем расчетную схему (направление токов в ветвях совпадает с направлением источников ЭДС). Электрическая схема спараметрами цепи и при данном графе, приведена на рисунке 2.15.
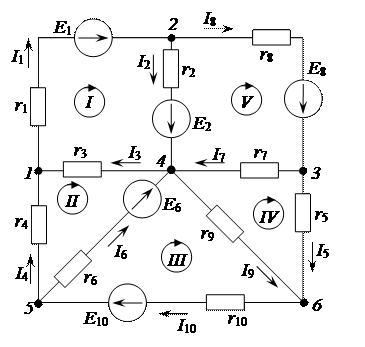
Рисунок 2.15 – Электрическая цепь
1.4. По приведенному на рисунке 2.16 графу, составленному при условии, что напряжения на зажимах каждой из ветвей, совпадает с направлением токов в этих ветвях, восстанавливаем матрицу соединений А.
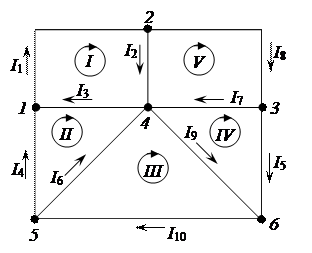
Рисунок 2.16 – Граф электрической цепи
Для приведенного графа, матрицу соединений Аимеет вид
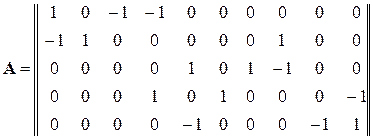 .
.
2. Составляем уравнения по законам Кирхгофа.
2.3. По первому закону Кирхгофа.
Произведение матрицы соединении А на матрицу-столбец токов ветвей 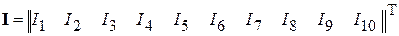 , дает совокупность левых частей уравнений, составленных по первому закону Кирхгофа
, дает совокупность левых частей уравнений, составленных по первому закону Кирхгофа
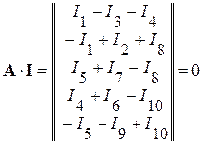 .
.
Таким образом,
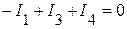 (1 узел);
(1 узел);
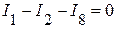 (2 узел);
(2 узел);
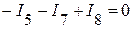 (3 узел);
(3 узел);
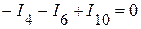 (4 узел);
(4 узел);
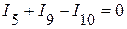 (5 узел).
(5 узел).
2.2. По второму закону Кирхгофа.
Произведение матрицы контуров В на матрицу-столбец напряжений ветвей 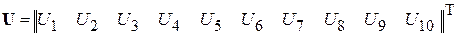 , дает совокупность левых частей уравнений, составленных по второму закону Кирхгофа
, дает совокупность левых частей уравнений, составленных по второму закону Кирхгофа
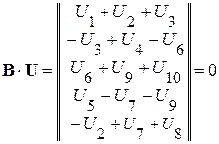 .
.
Таким образом,
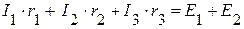 (I контур);
(I контур);
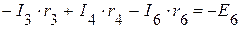 (II контур);
(II контур);
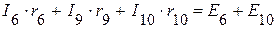 (III контур);
(III контур);
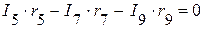 (IV контур);
(IV контур);
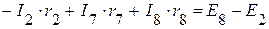 (V контур).
(V контур).
3. Подставляем числовые значения в полученную систему уравнений:
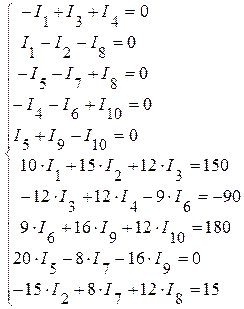
Решая данную систему уравнений, определяем токи в ветвях:
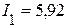 А,
А, 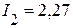 А,
А, 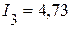 А,
А, 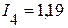 А,
А, 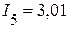 А,
А,
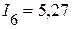 А,
А, 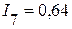 А,
А, 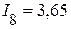 А,
А, 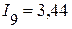 А,
А, 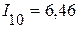 А.
А.
4. Проверяем решение системы уравнений, составив баланс мощностей.
4.1. Мощность источников:
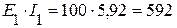 Вт,
Вт,
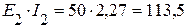 Вт,
Вт,
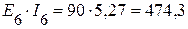 Вт,
Вт,
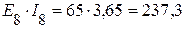 Вт,
Вт,
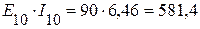 Вт.
Вт.
Суммарная мощность источников:
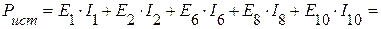
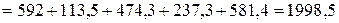 Вт.
Вт.
4.2. Мощность приемников:
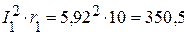 Вт,
Вт,
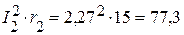 Вт,
Вт,
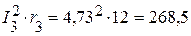 Вт,
Вт,
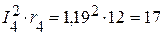 Вт,
Вт,
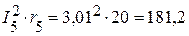 Вт,
Вт,
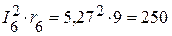 Вт,
Вт,
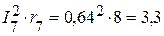 Вт,
Вт,
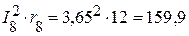 Вт,
Вт,
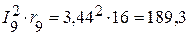 Вт,
Вт,
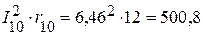 Вт.
Вт.
Суммарная мощность приемников:
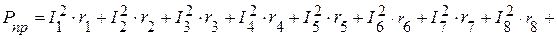
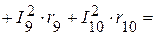
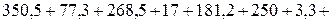
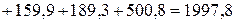 Вт.
Вт.
4.3. Из сравнения генерируемой мощности источниками и потребляемой мощности приемниками, следует, что погрешность вычислений 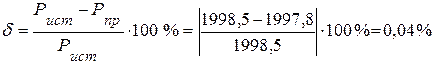 и не превышает 0,5%.
и не превышает 0,5%.
Дата добавления: 2016-08-23; просмотров: 10242;











