Уравнения для описания процессов электрической цепи. Законы Кирхгофа

Процессы, происходящие в электрических цепях, могут быть описаны системой уравнений состояния. Такими являются законы Кирхгофа.

Первый закон Кирхгофа:алгебраическая сумма токов ветвей, подсоединённых к одному узлу, равняется нулю: .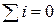

Для каждого узла принимают положительное и отрицательное направление тока в подсоединенных ветвях (например, если ток направлен к узлу, то перед соответствующим током ставят знак « + », если ток направлен от узла то – знак « - »).

Уравнения, составленные по первому закону Кирхгофа для электрической цепи, приведенной на рисунке 1.18, имеют вид:

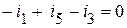(1 узел);

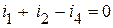(2 узел);

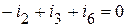(3 узел);

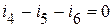(4 узел).

Если просуммировать приведенные выше уравнения для первого, второго и третьего узлов, то полученная сумма будет равна выражению, составленному по первому закону Кирхгофа для четвертого узла – .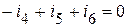

Следовательно, число независимых уравнений, составляемых по первому закону Кирхгофа равно ( ).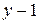

Второй закон Кирхгофа: алгебраическая сумма напряжений ветвей произвольного контура равна нулю.

Число независимых уравнений схемы равно числу главных контуров. Уравнения для остальных контуров могут быть получены из уравнений независимых контуров.

При составлении уравнений, составленных по второму закону Кирхгофа пользуются следующим правилом:если положительное направление обхода контура и направление тока на элементе совпадают, то напряжение в соответственной ветви принимается со знаком «+», если не совпадает – то со знаком «–».

Составим уравнения по второму закону Кирхгофа для электрической цепи, приведенной на рисунке 1.18:

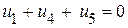(I контур);

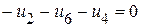(II контур);

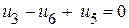(III контур).

Уравнения, составленные по второму закону Кирхгофа, могут быть описаны с использованием напряжений на элементах ветвей, входящих в контур. В этом случае второй закон Кирхгофа звучит так: алгебраическая сумма напряжений на элементах произвольного контура, равна алгебраической сумме ЭДС этого контура.

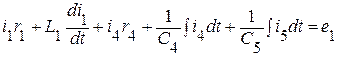(I контур);

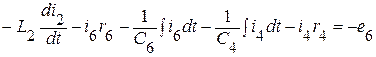(II контур);

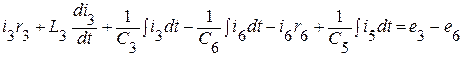(III контур).

Уравнения, полученные по первому и второму законам Кирхгофа, позволяют описать процессы в электрической схеме в любой момент времени. Их число равно количеству ветвей. Для данной схемы - 6.

Характер полученной системы уравнений – интегрально-дифференциальный. Если уравнение состоит только из резистивных элементов, то система уравнений имеет алгебраический характер.