Перевірка на рівність двох коефіцієнтів регресії
Припустимо, що в множинній регресії
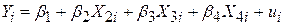
| (7.3.1) |
ми хочемо перевірити гіпотези
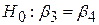 або або 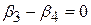 , ,
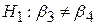 або або 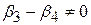
| (7.3.2) |
про рівність двох кутових коефіцієнтів.
Подібна гіпотеза має важливе практичне значення. Наприклад, хай у моделі (7.3.1) представлена функція попиту на товар. У ній Y – величина попиту на товар, X2 – ціна товару, X3 – дохід покупця, X4 – статки покупця. Нульова гіпотеза в цьому випадку означає, що коефіцієнти з доходу й статків збігаються. Або якщо 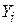 і змінні X виражені в логарифмічному вигляді
і змінні X виражені в логарифмічному вигляді
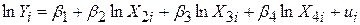 , ,
|
то нульова гіпотеза (7.3.2) припускає, що еластичності за доходом і статками однакові.
Як перевірити цю гіпотезу? Можна показати, що при виконанні звичайних класичних припущень величина
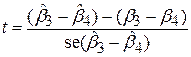
| (7.3.3) |
випливає із закону t-розподілуз (n–4) степенями вільності, оскільки (7.3.1) являє собою модель із 4 змінними. У загальному випадку моделі з k параметрами кількість степенів вільності дорівнює (n–k). Величина 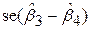 , що входить в (7.3.3) обчислюється за формулою
, що входить в (7.3.3) обчислюється за формулою
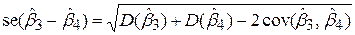 . .
| (7.3.4) |
З урахуванням нульової гіпотези можна подати (7.3.3) у вигляді
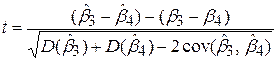 . .
| (7.3.5) |
Процедура використання t-статистикиза (7.3.5) нічим не відрізняється від уже нам відомої. Якщо визначена за (7.3.5) величина t перевищує критичне значення для вибраного рівня значущості і відповідної кількості степенів вільності, то ми відхиляємо нульову гіпотезу; в протилежному випадку гіпотеза не відхиляється. Можна застосувати після визначення t за (7.3.5)і підхід на підставі p-величини.
Розглянемо приклад, до якого ми зверталися раніше, кубічної функції вартості:
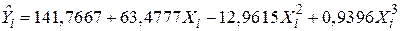 Se=(6,3753) (4,7786) (0,9857) (0,0591)
Se=(6,3753) (4,7786) (0,9857) (0,0591)
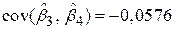 ,R2=0,9983, ,R2=0,9983,
|
де Y – загальні витрати; Х – обсяг продукції, що випускається.
Припустимо, ми хочемо перевірити гіпотезу про те, що коефіцієнти при Х2 і Х3 у функції вартості збігаються, тобто 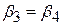 або
або 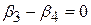 . За наведеними даними підрахуємо значення t:
. За наведеними даними підрахуємо значення t:
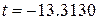 . .
|
Легко перевірити, що для DF=6отримане значення t перевершує критичне значення навіть при a=0,002 (або 0,2%). Отже, ми можемо відхиляти гіпотезу про рівність у кубічній функції вартості коефіцієнтів при Х2 і Х3.
Дата добавления: 2016-07-27; просмотров: 1639;











