Додатковий або граничний внесок пояснювальної змінної
Повернемося до ілюстрованого прикладу. З (7.2.2) ми знаємо, що коефіцієнти при Х2 (дохід) і при Х3 (тренд) значущо відрізняються від нуля на основі роздільних t-тестів. Ми також бачили, що на підставі F-тестів (7.2.7) і (7.2.13) сама лінія регресії також значуща. Припустимо тепер, що ми вводимо X2 і X3 послідовно, тобто ми спочатку проводимо регресію Y за Х2 і оцінюємо її значущість, а потім додаємо до моделі Х3 і визначаємо, наскільки її внесок виявляється істотним (зрозуміло, що порядок, у якому змінні вводяться в модель, може бути змінений на протилежний). Під внеском ми розуміємо таке: Чи приводить додавання змінної до моделі до зростання ESS (і R2) значущо в порівнянні з RSS. Цей внесок можна назвати додатковим або граничним внеском пояснювальної змінної.
Дослідження питання про додатковий внесок змінної має важливе практичне значення. У більшості емпіричних досліджень може бути не зовсім зрозуміло, чи варто додавати до моделі змінну Х крім інших змінних, включених в модель. Не слід включати в модель змінну, внесок якої в ESS незначний, і виключати з моделі змінну, що має в ESS істотний внесок. Як же визначити, наскільки істотно змінна X зменшує RSS? Розвиток техніки аналізу дисперсій дозволяє легко відповісти на це питання.
Припустимо, що ми спочатку проводимо регресію Y (особисті витрати на споживання) за X2 (особистий дохід) і одержуємо таку регресію:
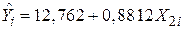 (4,6818) (0,0114)
t = (2,7259) (77,2982)
R2=0,9978,
(4,6818) (0,0114)
t = (2,7259) (77,2982)
R2=0,9978, 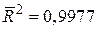
| (7.2.14) |
Згідно з нульовою гіпотезою 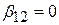 , а отже t=77.2982. Очевидно, що
, а отже t=77.2982. Очевидно, що 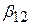 значущо відрізняється від нуля як при 5%-му рівні значущості, так і при 1%-му рівні. Таким чином, Х2 значущо впливає на Y. Таблиця ANOVA регресії (7.2.14) подана нижче.
значущо відрізняється від нуля як при 5%-му рівні значущості, так і при 1%-му рівні. Таким чином, Х2 значущо впливає на Y. Таблиця ANOVA регресії (7.2.14) подана нижче.
Таблиця 7.4
ANOVA-таблиця для регресії (7.2.14)
| Джерело дисперсії | SS | DF | MSS |
| ESS | 65898,2353 | 65898,2353 | |
| RSS | 144,0340 | 11,0800 | |
| Загальна | 66042,2693 |
Припускаючи нормальність закону розподілу збурень 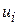 і нульову гіпотезу
і нульову гіпотезу 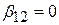 , ми маємо, що F=5947.494 згідно із законом F-розподілу з 1 і 13 степенями вільності.
, ми маємо, що F=5947.494 згідно із законом F-розподілу з 1 і 13 степенями вільності.
Очевидно, що знайдене значення F свідчить про значущість 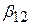 при загальноприйнятих рівнях значущості. Таким чином, так як і раніше, ми можемо відхиляти гіпотезу про
при загальноприйнятих рівнях значущості. Таким чином, так як і раніше, ми можемо відхиляти гіпотезу про 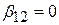 . Побіжно зазначимо, що T2=(77.2982)2=5947.494. Цей результат очікуваний, оскільки ми знаємо, що при однаковій нульовій гіпотезі й однаковому рівні значущості квадрат величини t з (n–2) степенями вільності рівний величині F з 1 і (n–2) степеням вільності.
. Побіжно зазначимо, що T2=(77.2982)2=5947.494. Цей результат очікуваний, оскільки ми знаємо, що при однаковій нульовій гіпотезі й однаковому рівні значущості квадрат величини t з (n–2) степенями вільності рівний величині F з 1 і (n–2) степеням вільності.
Припустимо, що після отримання регресії (7.2.14) ми ви рішили додати до моделі змінну Х3 (тренд) і отримали множинну регресію (7.2.2). При цьому слід отримати відповіді на такі питання. Який додатковий внесок у модель змінної Х3 в порівнянні з моделлю (7.2.14)? Чи є отримана в порівнянні з моделлю (7.2.14), добавка статистично значущою? Який критерій для включення в модель додаткових змінних? Відповіді на ці питання можна отримати на підставі аналізу дисперсій. Для цього розглянемо табл. 7.5.
Таблиця 7.5
ANOVA-таблиця для оцінки додаткового внеску змінної.
| Джерело дисперсії | SS | DF | MSS |
| ESSунаслідок Х2 | 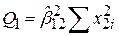
| Q1/1 | |
| ESS унаслідок Х3 | Q2=Q3–Q1 | Q2/1 | |
| ESS унаслідок Х2 і Х3 | 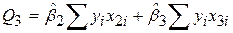
| Q3/2 | |
| RSS | Q4=Q5–Q3 | N–3 | Q4/(N–3) |
| Загальна | 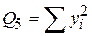
| N–1 |
Для даного прикладу одержуємо такі результати (табл. 7.6).
Таблиця 7.6
| Джерело дисперсії | SS | DF | MSS |
| ESS унаслідок Х2 | Q1=65898,2353 | 65898,2353 | |
| ESS унаслідок Х3 | Q2=66,8647 | 66,8647 | |
| ESS унаслідок Х2 і Х3 | Q3=65965,100 | 32892,55 | |
| RSS | Q4=77,1693 | 6,4302 | |
| Загальна | Q5=66042,2693 |
Для отримання оцінки додаткового внеску від X3 до вже врахованої змінної X2 підраховуємо
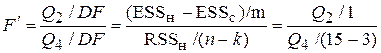 , ,
| (7.2.15) |
де ESSн – оцінена сума квадратів нової моделі (тобто після додавання нових регресорів); ESSс – оцінена сума квадратів старої моделі (Q1); RSSн – сума квадратів залишків (Q4); m – кількість нових регресорів; k – кількість параметрів у новій моделі.
Для нашого прикладу одержуємо
| F=10,3973. | (7.2.16) |
Тепер при звичайних припущеннях про нормальність 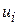 і нульовій гіпотезі
і нульовій гіпотезі 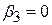 можна показати, що підрахована за (7.2.15) величина F підкоряється закону F-розподілуз 1 і 12 степенями вільності.
можна показати, що підрахована за (7.2.15) величина F підкоряється закону F-розподілуз 1 і 12 степенями вільності.
Побіжно відзначимо, що величину F з (7.2.15) можна подати тільки через значення R2, як це було зроблено в (7.2.13). Одержуємо вираз
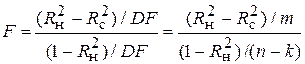 . .
| (7.2.17) |
Для нашого прикладу, застосовуючи (7.2.2) і (7.2.14), отримуємо
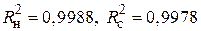 . .
|
Отже,
| F=10,973. | (7.2.18) |
Таким чином, на підставі будь-якого з F-тестів, ми можемо відкинути нульову гіпотезу і зробити висновок, що додавання в модель Х3 значущо підвищує ESS і, отже, R2. Висновок: змінну тренда Х3 слід додати в модель.
Пригадаємо, що в (7.2.2) ми отримали t=3,246для коефіцієнта при Х3 при гіпотезі 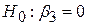 . Зазначимо, що t2=10,973=F. Це співвідношення очевидне, якщо врахувати зв’язок між F і t2, згадуваний раніше.
. Зазначимо, що t2=10,973=F. Це співвідношення очевидне, якщо врахувати зв’язок між F і t2, згадуваний раніше.
Описана процедура F-теста дає формальний метод ухвалення рішення про те, чи варто включати додаткову змінну в модель регресії. Часто дослідники стикаються із задачею вибору найкращої з моделей, що мають однакову пояснювану змінну, але різні пояснювальні. Багато хто як критерій вибору використовує величину  , тобто вибирають модель із найбільшим
, тобто вибирають модель із найбільшим  . Отже, включення змінної спричиняє зростання
. Отже, включення змінної спричиняє зростання  , вона зберігається в моделі, хоча й не зменшує RSS значущо в статистичному значенні. У такому разі виникає питання: коли
, вона зберігається в моделі, хоча й не зменшує RSS значущо в статистичному значенні. У такому разі виникає питання: коли  зростає? Можна показати, що
зростає? Можна показати, що  зростатиме, якщо величина t для коефіцієнта при новій доданій в модель змінній за абсолютною величиною більше 1, де t – статистика, підрахована при нульовій гіпотезі про рівність нулю відповідного коефіцієнта. Наведений критерій може бути сформульований й інакше.
зростатиме, якщо величина t для коефіцієнта при новій доданій в модель змінній за абсолютною величиною більше 1, де t – статистика, підрахована при нульовій гіпотезі про рівність нулю відповідного коефіцієнта. Наведений критерій може бути сформульований й інакше.  зростатиме з додаванням нової пояснювальної змінної, якщо F (=t2) цієї змінної більше 1.
зростатиме з додаванням нової пояснювальної змінної, якщо F (=t2) цієї змінної більше 1.
За цим критерієм змінна тренда Х3 з t=3.2246 або F=10.3973повинна приводити до зростання  , що насправді й відбувається. З її одаванням
, що насправді й відбувається. З її одаванням  зростає з 0,9977 до 0,9986.
зростає з 0,9977 до 0,9986.
Чи можна поширити наведений критерій на групу коефіцієнтів, що додаються? Відповідь очевидна з (7.2.17). Якщо додавання до моделі групи змінних дає величину F більше 1, то  при цьому зростає.
при цьому зростає.
Дата добавления: 2016-07-27; просмотров: 1751;











