Перевірка лінійних обмежень
Бувають випадки, коли економічна теорія припускає, що коефіцієнти в рівнянні регресії задовольняють деяким, лінійним обмеженням. Розглянемо, наприклад, продуктивну функцію Коба-Дугласа
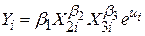 , ,
| (7.4.1) |
де 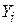 – вироблена продукція; Х2 – трудовитрати; Х3 – капіталозатрати; ui – стохастичний збурюючий складова. Після переходу до логарифмічних змінних, одержуємо
– вироблена продукція; Х2 – трудовитрати; Х3 – капіталозатрати; ui – стохастичний збурюючий складова. Після переходу до логарифмічних змінних, одержуємо
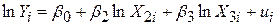 , ,
| (7.4.2) |
де 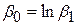 .
.
Економічна теорія припускає, що
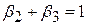 . .
| (7.4.3) |
Рівність (7.4.3) являє собою приклад лінійного обмеження.
Для перевірки постійного зростання доходу, тобто справедливості обмеження (7.4.3) можна застосовувати два підходи.
Перший підхід ґрунтується на t-тесті. При цьому спочатку проводиться оцінка рівняння (7.4.2) без урахування обмеження (7.4.3). Називатимемо цю регресію регресією без обмежень. Отримавши оцінки 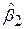 і
і 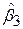 за МНК, проведемо перевірку виконання гіпотези (7.4.3) на підставі t-тесту (див. 7.3.5):
за МНК, проведемо перевірку виконання гіпотези (7.4.3) на підставі t-тесту (див. 7.3.5):
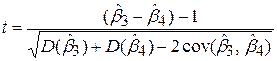 . .
| (7.4.4) |
Згідно з процедурою перевірки гіпотези порівняємо (7.4.4) з критичним значенням t-розподілудля (n–k) степенів вільності (у нашому випадку n–3) і вибраного рівня значущості a, якщо t з (7.4.4) перевершує критичне значення, то гіпотеза відкидається, у протилежному випадку – не відкидається.
Описана процедура має ту особливість, що спочатку проводиться регресія, а перевірка лінійного обмеження (7.4.3) здійснюється на підставі результатів регресії без обмежень. Можливий інший підхід, коли лінійне обмеження в (7.4.3) враховується із самого початку. У нашому випадку подамо (7.4.3) у вигляді
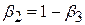
| (7.4.5) |
або
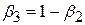 . .
| (7.4.6) |
Застосовуючи одне з цих рівнянь, можна виключити один з коефіцієнтів регресії в рівнянні (7.4.2). Якщо застосувати (7.4.5), то можна подати виробничу функцію (7.4.2) у вигляді
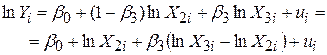
|
або
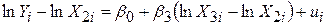 ; ;
| (7.4.7) |
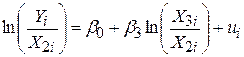 , ,
| (7.4.8) |
де 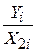 – відношення обсягу продукції до трудовитрат, а
– відношення обсягу продукції до трудовитрат, а 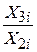 – коефіцієнт відношення капіталу до трудовитрат.
– коефіцієнт відношення капіталу до трудовитрат.
Звернемо увагу на те, як змінилося початкове рівняння (7.4.2). Якщо ми проведемо оцінку 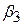 з (7.4.8), то ми легко можемо знайти
з (7.4.8), то ми легко можемо знайти  за рівністю (7.4.5). Зайве говорити, що подібна процедура гарантує дорівнюваність одиниці суми коефіцієнтів регресії. Описана процедура називається регресією з обмеженнями. Цей метод може бути поширений на моделі, що містять будь-яку кількість пояснювальних змінних і більш ніж одну умову типу (7.4.3).
за рівністю (7.4.5). Зайве говорити, що подібна процедура гарантує дорівнюваність одиниці суми коефіцієнтів регресії. Описана процедура називається регресією з обмеженнями. Цей метод може бути поширений на моделі, що містять будь-яку кількість пояснювальних змінних і більш ніж одну умову типу (7.4.3).
Як ми можемо порівняти результати регресії без обмежень з обмеженими? Іншими словами, як визначити чи виконується лінійне обмеження (7.4.3)? На це питання можна відповісти після проведення F-тесту.
Введемо деякі позначення:
- 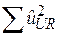 – сума квадратів залишків регресії (7.4.2) без обмежень;
– сума квадратів залишків регресії (7.4.2) без обмежень;
- 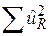 – сума квадратів залишків регресії з обмеженнями (7.4.8);
– сума квадратів залишків регресії з обмеженнями (7.4.8);
- m – кількість лінійних обмежень (у нашому випадку m=1);
- n – кількість спостережень.
Обчислимо
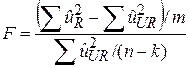 . .
| (7.4.9) |
Можна показати, що обчислена величина підкоряється закону F-розподілу з m і (n–k) степенями вільності.
Наведений вище F-тестможна виразити і в R2. У такому випадку маємо вираз
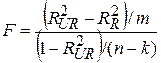 . .
| (7.4.10) |
Тут 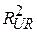 і
і 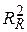 позначають коефіцієнти детермінації регресії без обмежень (7.4.2) і з обмеженнями (7.4.8) відповідно. Побіжно зазначимо, що
позначають коефіцієнти детермінації регресії без обмежень (7.4.2) і з обмеженнями (7.4.8) відповідно. Побіжно зазначимо, що
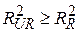 , , 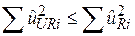 . .
|
Нагадаємо також, що оскільки в регресії без обмежень і з обмеженнями залежні змінні не збігаються, то не можна безпосередньо порівнювати коефіцієнти детермінації 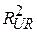 і
і 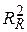 .
.
Дата добавления: 2016-07-27; просмотров: 1729;











