Перевірка вибіркової регресії на загальну значущість
У попередньому підрозділі ми зосередили свою увагу на перевірці на значущість окремих оцінених частинних коефіцієнтів регресії, тобто перевірялася гіпотеза, що окремо взятий коефіцієнт регресії дорівнює нулю. Зараз ми розглянемо гіпотезу
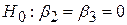 . .
| (7.2.1) |
Дана нульова гіпотеза припускає, що коефіцієнти  і
і 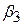 одночасно дорівнювати нулю. Перевірка подібної гіпотези називається перевіркою на загальну значущість оціненої лінії регресії, тобто перевіркою на зв’язок Y і змінних X2 і X3.
одночасно дорівнювати нулю. Перевірка подібної гіпотези називається перевіркою на загальну значущість оціненої лінії регресії, тобто перевіркою на зв’язок Y і змінних X2 і X3.
Чи можна замінити перевірку гіпотези (7.2.1) перевіркою на значущість кожного окремого коефіцієнта  і
і 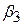 ? Відповідь на це питання негативна з таких причин.
? Відповідь на це питання негативна з таких причин.
При перевірці на індивідуальну значущість отриманих частинних коефіцієнтів регресії ми неявно припускали, що кожен тест на значущість ґрунтується на незалежній вибірці. Так, при перевірці на значущість коефіцієнта 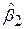 при нульовій гіпотезі
при нульовій гіпотезі 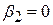 неявно передбачається, що тестування ґрунтується на даних іншої вибірки стосовно вибірки, що використовується для перевірки гіпотези про
неявно передбачається, що тестування ґрунтується на даних іншої вибірки стосовно вибірки, що використовується для перевірки гіпотези про 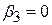 . Але для перевірки спільної гіпотези (7.2.1) при використанні даних табл. 6.1 ми порушуємо припущення, на якому ґрунтується процедура тестування. Ми можемо розглядати це питання й інакше. Нерівність (7.1.2) задає 95%-й довірчий інтервал для коефіцієнта
. Але для перевірки спільної гіпотези (7.2.1) при використанні даних табл. 6.1 ми порушуємо припущення, на якому ґрунтується процедура тестування. Ми можемо розглядати це питання й інакше. Нерівність (7.1.2) задає 95%-й довірчий інтервал для коефіцієнта  . Але якщо ми використовуємо ті ж вибіркові дані для знаходження 95%-го довірчого інтервалу для коефіцієнта
. Але якщо ми використовуємо ті ж вибіркові дані для знаходження 95%-го довірчого інтервалу для коефіцієнта 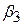 , то ми не можемо стверджувати, що обидва коефіцієнти
, то ми не можемо стверджувати, що обидва коефіцієнти  і
і 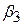 лежать усередині відповідних довірчих інтервалів із вірогідністю (1–a)´(1–a)=0,90.
лежать усередині відповідних довірчих інтервалів із вірогідністю (1–a)´(1–a)=0,90.
Іншими словами, хоча твердження
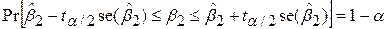 ; ;
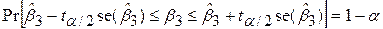
|
індивідуально справедливі, однак несправедливе твердження про те, що вірогідність одночасного потрапляння коефіцієнтів  і
і 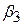 в інтервали
в інтервали  ,
, 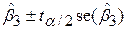 є (1–a)2, оскільки ці інтервали можуть не бути незалежними при використовуванні однакових даннях при їх знаходженні.
є (1–a)2, оскільки ці інтервали можуть не бути незалежними при використовуванні однакових даннях при їх знаходженні.
Перевірка на загальну значущість множинної регресії на підставі аналізу дисперсії. F–тестування
Ми вже говорили, що t-тест не дозволяє судити про загальну значущість множинної регресії. Для цього застосовується підхід, який базується на аналізі дисперсії (ANOVA), розглянутий нами раніше для моделі з двома змінними. Даний підхід застосовується і в разі множинної регресії.
Пригадаємо, що
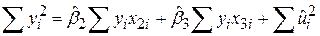 ; ;
| (7.2.2) |
TSS=ESS+RSS.
Як уже раніше наголошувалося, TSSмає (n–1) степенів вільності, RSS – (n–3), а ESS – 2 степені. Повторюючи знайому нам процедуру аналізу дисперсії, складаємо таку ANOVA-таблицю:
Таблиця 7.1
ANOVA-таблиця для регресії з трьома змінними
| Джерело дисперсії | Сума квадратів | DF | Середня сума квадратів |
| За регресією (ESS) | 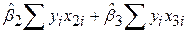
| 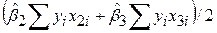
| |
| За залишками (RSS) | 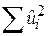
| N–3 | 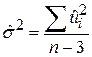
|
| Загальна | 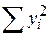
| N–1 |
Можна показати, що при припущенні нормальності розподілу залишків 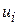 і нульовій гіпотезі
і нульовій гіпотезі  змінна
змінна
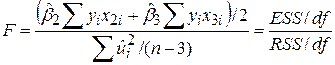
| (7.2.3) |
підкоряється закону F-розподілу з 2 і (n–3) степенями вільності.
При припущенні, що 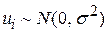 , справедлива рівність
, справедлива рівність
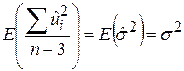 . .
| (7.2.4) |
Додатково припустивши, що  , можна також показати, що
, можна також показати, що
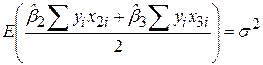 . .
| (7.2.5) |
Отже, якщо нульова гіпотеза виконується, то обидві рівності (7.2.4) і (7.2.5) дають ідентичні оцінки для 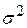 . Оскільки через зв’язок, існуючий між Y, Х2 і Х3, єдиним джерелом дисперсії Y є випадкова складова
. Оскільки через зв’язок, існуючий між Y, Х2 і Х3, єдиним джерелом дисперсії Y є випадкова складова 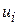 . Якщо ж нульова гіпотеза несправедлива, тобто Х2 і Х3 безумовно впливають на у, еквівалентність між (7.2.4) і (7.2.5) виконуватися не буде. У такому випадку величина ESS буде порівняно більша, ніж RSS, враховуючи кількість їх степенів вільності. Отже, величина F, визначувана рівністю (7.2.3), може служити тестом на перевірку нульової гіпотези про те, що кутові коефіцієнти
. Якщо ж нульова гіпотеза несправедлива, тобто Х2 і Х3 безумовно впливають на у, еквівалентність між (7.2.4) і (7.2.5) виконуватися не буде. У такому випадку величина ESS буде порівняно більша, ніж RSS, враховуючи кількість їх степенів вільності. Отже, величина F, визначувана рівністю (7.2.3), може служити тестом на перевірку нульової гіпотези про те, що кутові коефіцієнти 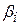 одночасно перетворюються в нуль. Якщо підрахована за (7.2.3) величина F більша, ніж визначене за таблицею критичне для вибраного рівня значущості значення, то ми відкидаємо гіпотезу Н0, в іншому випадку – не відкидаємо. Альтернативою служить використання р–величини. Якщо отримане з використанням F значення p–величини достатньо мале, ми можемо відхиляти гіпотезу Н0.
одночасно перетворюються в нуль. Якщо підрахована за (7.2.3) величина F більша, ніж визначене за таблицею критичне для вибраного рівня значущості значення, то ми відкидаємо гіпотезу Н0, в іншому випадку – не відкидаємо. Альтернативою служить використання р–величини. Якщо отримане з використанням F значення p–величини достатньо мале, ми можемо відхиляти гіпотезу Н0.
Наведемо дані аналізу дисперсії для нашого прикладу (табл. 7.2).
Таблиця 7.2
| Джерело дисперсії | Сума квадратів | DF | Середнє значення |
| За регресією | 65965.1003 | 32982,5502 | |
| За залишками | 77.1690 | 6,4308 | |
| Усього | 66042.2693 |
За даними з табл.7.2 знаходимо
 . .
| (7.2.6) |
Якщо ми візьмемо a=0.05, то критичне значення F для 2 і 12 степенів вільності буде F0.05(2, 12)=3,88529. Очевидно що підрахована величина F значуща і ми можемо, отже, відхиляти нульову гіпотезу. Якщо вибрати рівень значущості a=0.01, то F0.01(2, 12)=6.9266. Підрахована нами величина F залишається значно перевершуючою це критичне значення. Ми, як і раніше, відхиляємо нульову гіпотезу. Побіжно зазначимо, що p–величина, відповідна значенню F, украй мала (2.545×10–18).
Описану процедуру F–тестування можна узагальнити на випадок множинної регресії з k змінними.
Хай задана розглянута модель з k змінними
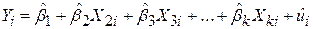 . .
|
Для перевірки гіпотези
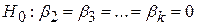
і альтернативної гіпотези
Н1: не всі кутові коефіцієнти одночасно дорівнюють нулю
підрахуємо
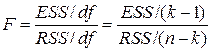 . .
| (7.2.7) |
Якщо F>Fa(k–1, n–k), відхиляємо гіпотезу Н0; у протилежному випадку – не відхиляємо. Тут Fa(k–1, n–k) – критичне значення величини F для заданого рівня значущості a, (k–1) – кількість степенів вільності в чисельнику і (n–k) – кількість степенів вільності в знаменнику. За альтернативним підходом, якщо відповідна F величина p достатньо мала, відхиляємо гіпотезу Н0.
Зв’язок між R2 і F
Існує внутрішній зв’язок між коефіцієнтом детермінації R2 і F-тестуванням, що використовується в аналізі дисперсії. Припускаючи нормальний закон розподілу збурень 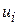 і приймаючи нульову гіпотезу про те, що
і приймаючи нульову гіпотезу про те, що  , ми бачимо, що
, ми бачимо, що
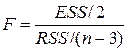
| (7.2.8) |
розподілена за законом F-розподілу з 2 і (n–3) степенями вільності.
Для загального випадку моделі з k змінними, припускаючи нормальний закон розподілу залишків і приймаючи нульову гіпотезу
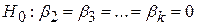
| (7.2.9) |
отримуємо, що
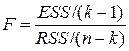
| (7.2.10) |
розподілене за законом F-розподілу з (k–1) і (n–k) степенями вільності. Перетворивши (7.2.10), отримаємо
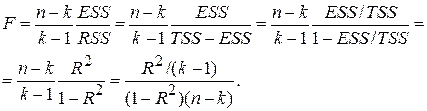
| (7.2.11) |
При цьому ми спиралися на той факт, що 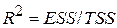 . Із рівняння (7.2.11) бачимо, що величини F і R2 пов’язані безпосередньо. Якщо R2=0, то й F=0. Чим більше R2, тим більше F. У межі при
. Із рівняння (7.2.11) бачимо, що величини F і R2 пов’язані безпосередньо. Якщо R2=0, то й F=0. Чим більше R2, тим більше F. У межі при  ,
,  .
.
Для випадку моделі з трьома змінними (7.2.11) набуває вигляду
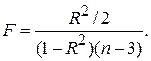
| (7.2.12) |
Враховуючи тісний зв’язок між F і R2, ANOVA-таблиця може бути перетворена до вигляду табл. 7.3.
Таблиця 7.3
ANOVA-таблиця в термінах R2
| Джерело дисперсії | SS | DF | MSS |
| За регресією | 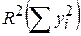
| 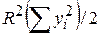
| |
| За залишками | 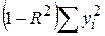
| N–3 | 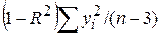
|
| Загальна | 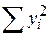
| N–1 |
Наведемо правило перевірки на загальну значущість множинної регресії в термінах R2.
Правило ухвалення рішення.Хай задана модель регресії з k змінними
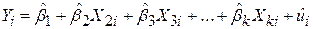 . .
|
Для перевірки гіпотези
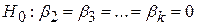
і альтернативної їй гіпотези
Н1: не всі кутові коефіцієнти одночасно дорівнюють нулю
підраховуємо
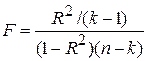 . .
| (7.2.13) |
Якщо F>Fa(k–1, n–k), відхиляємо гіпотезу Н0, у протилежному випадку можна прийняти Н0. Можна скористатися підходом, що базується на обчисленні p-величини. Якщо отримана відповідно до (7.2.13) p-величина достатньо мала, ми відхиляємо гіпотезу Н0.
Дата добавления: 2016-07-27; просмотров: 1802;











