Приклад. Попит на курятину в США, 1960–1982.

Розглянемо таку модель попиту на курятину:

,

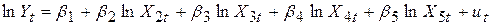де Y – попит на курятину на душу населення; Х₂ – реальний дохід, на душу населення, Х₃ – роздрібна ціна на курятину за фунт, Х₄ – роздрібна ціна на свинину за фунт, Х₅ – роздрібна ціна на яловичину за фунт.

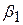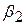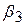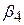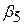У цій моделі , , , і є еластичностями за доходом, власною ціною, крос-ціною (свинина) і крос-ціною (яловичина) відповідно. Згідно з економічною теорією

;

;

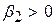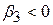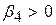, якщо курятина й свинина є конкуруючими продуктами;

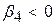, якщо курятина й свинина є взаємодоповнюючими продуктами;

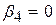, якщо курятина й свинина є незв’язаними продуктами;

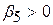, якщо курятина й яловичина є конкуруючими продуктами;

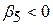, якщо курятина й яловичина є взаємодоповнюючими продуктами;

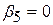, якщо курятина й яловичина є незв’язаними продуктами.

Припустимо, хтось вважає, що курятина й свинина, курятина й яловичина є незв’язаними продуктами в тому значенні, що на попит курятини не впливають ціни на свинину й яловичину. У прийнятих позначеннях це означає

.

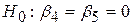(7.4.17)

З урахуванням цього регресія з обмеженнями набуває вигляду

.

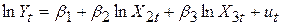(7.4.18)

Зрозуміло, що за нашою термінологію рівняння (7.4.19) є регресія без обмежень.

Якщо скористатися конкретними даними, то можна отримати такі результати.

Регресія без обмежень:

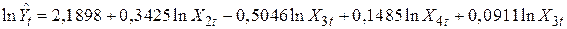(0,1557) (0,0833) (0,1109) (0,0997) (0,1007) .

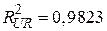(7.4.19)

Регресія з обмеженнями:

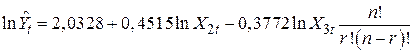(0,1162) (0,0247) (0,0635) .

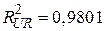(7.4.20)

У дужках указані значення стандартних похибок коефіцієнтів регресії. Зазначимо, що R² в (7.4.19) і (7.4.20) можна порівнювати, оскільки залежна змінна в обох моделях однакова.

Для перевірки гіпотези (7.4.17) необхідно підрахувати значення F за формулою (7.4.10):

.

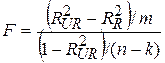У нашому випадку m=2, оскільки є два обмеження. Кількість степенів вільності знаменника дорівнює 18. З урахуванням цього, одержуємо

При 5%-му рівні значущості це значення не виявляється статистично значимим, оскільки F_0.05(2, 18)=3,55. Відповідне значення p=0,3472. Отже, ми не маємо підстав відхиляти нульову гіпотезу – попит на курятину не залежить від ціни на свинину та яловичину.

Відзначимо, що отримана функція попиту на курятину відповідає нашим апріорним очікуванням, оскільки еластичність за доходом позитивна. Оцінена еластичність за ціною виявляється за абсолютною величиною статистично менше 1, тобто попит на курятину нееластичний за ціною. Еластичність за доходом, хоча й позитивна, так само виявляється статистично менше 1.