Приклад. Виробнича функція Коба–Дугласа для агросектору Тайваню в 1958–1972 рр.

Проілюструємо викладений вище підхід прикладом виробничої функції для агросектора Тайваню в 1958–1972 рр. (див. табл. 5.3).

Результати регресії за моделлю без обмежень подані формулами (7.10.4). Тепер припустимо, що ми накладаємо обмеження 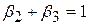і застосовуємо модель (7.4.8). У результаті одержуємо

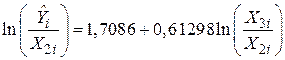(0,4159) (0,0933) , .

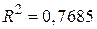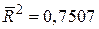(7.4.11)

Відзначимо, що величини R² в (7.10.4) і (7.4.11) не можна порівнювати, оскільки праві частини рівнянь мають різний вигляд. Для їх порівняння потрібно виконати процедуру, описану в розд. 5 . Якщо застосувати даний прийом, то для моделі (7.4.13) ми одержуємо R²=0,8489, що виявляється менше, ніж R²=0,8890 в моделі (7.12.4) без обмежень.

Отже, з (7.10.4) ми отримали 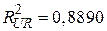, а з (7.4.13) – 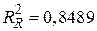. Тепер ми можемо застосувати F-тест (7.4.10):

.

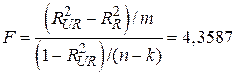(7.4.12)

Дана величина F підкоряється закону F-розподілуз 1 і 12 степенями вільності. Із таблиць розподілу Фішера знаходимо, що F_0.05(1, 12)=4,75, але F_0.1(1, 12)=3,18. Таким чином, значення F=4,3587 не є значущим при a=0,05, але є таким при a=0,1. Якщо при дослідженні ми встановимо a=0,05, то гіпотезу 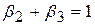ми відхилити не зможемо, а це означає, що період дослідження 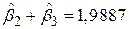не відрізняється значущо від 1. Цей приклад показує, наскільки важливо проводити формальну перевірку гіпотези, а не покладатися тільки на величину оцінених коефіцієнтів регресії. Даний випадок також нагадує, що ми повинні встановлювати рівень значущості до початку перевірки гіпотези, а не після її проведення. Як згадувалося раніше, доцільно наводити значення p-величини. У даному прикладі p=0,0588. Звідси бачимо, що F=4,3587 значуща для .

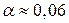УзагальненийF-тест

Формули (7.4.9), (7.4.10) представляють загальний метод перевірки гіпотез щодо параметрів моделі регресії з k змінними

.

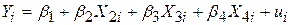(7.4.13)

F-тест (7.2.16) або t-тест (8.3.3) є не що інше, як спеціальний випадок (7.4.10). Наприклад, такі гіпотези, як

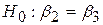;	(7.4.14)
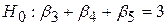,	(7.4.15)

що накладають декілька лінійних зв’язків на параметри моделі з k параметрами, або гіпотеза

,

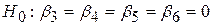(7.4.16)

стверджуюча, що деякі регресори, відсутні в моделі, можуть бути перевірені за допомогою F-тесту (7.4.10).

Загальна стратегія застосування F-тесту така. Є велика модель, модель без зв’язків (7.4.13), і є менша модель, модель зі зв’язками, яка виходить з більшої шляхом виключення з неї декількох змінних (випадок (7.4.16), або накладанням декількох зв’язків на коефіцієнти великої моделі (випадки (7.4.14) і (7.4.15)).

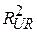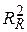Виконуємо регресію моделей без обмеження і з обмеженнями й одержуємо коефіцієнти детермінації і відповідно. Кількість степенів вільності в моделі без обмежень (n–k), а в моделі з обмеженнями m – кількість лінійних обмежень,1 у (7.4.16) або (7.4.17) і 4 у (7.4.18). Потім ми за (7.4.10) підраховуємо F і застосовуємо правило: якщо підраховане F більше 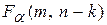, яке є критичним F для вибраного рівня значущості, ми відкидаємо нульову гіпотезу, у протилежному випадку – не відкидаємо.