Перевірка гіпотези про частинний коефіцієнт регресії
Якщо ми приймаємо гіпотезу про те, що 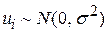 , тоді, як було відзначено раніше, ми можемо скористатися t-тестом для перевірки гіпотези щодо будь-якого частинного коефіцієнта регресії. Для ілюстрації механізму розглянемо наш числовий приклад. Припустимо, ми постулювали
, тоді, як було відзначено раніше, ми можемо скористатися t-тестом для перевірки гіпотези щодо будь-якого частинного коефіцієнта регресії. Для ілюстрації механізму розглянемо наш числовий приклад. Припустимо, ми постулювали
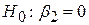 і і 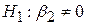 . .
|
Нульова гіпотеза твердить, що зберігаючи постійним значення Х3, особистий дохід не має лінійного впливу на особисті витрати на споживання. Для перевірки нульової гіпотези використовуємо t-тест, визначений рівністю (6.1.4). Відповідно до нашої методики ми перевіряємо, чи перевершує значення t-тесту критичне значення t-величини при вибраному нами рівні значущості. Якщо це так, то ми відкидаємо нульову гіпотезу, а в противному випадку – залишаємо. Для нашого прикладу, застосовуючи (6.1.4) і враховуючи, що згідно з нульовою гіпотезою 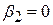 , одержуємо
, одержуємо
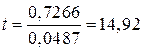 . .
| (7.1.1) |
Якщо ми візьмемо a=0,05, ta/2=2,179 для DF=12. Оскільки підрахована величина значно перевершує критичне значення tкр=2,179, ми можемо відкинути нульову гіпотезу і стверджувати, що 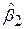 статистично значиме, тобто значно відрізняється від нуля. Більше того, як показано у (6.1.5), отримана за (7.1.1) відповідна p–величина вкрай мала. На рис. 7.1. описана вище процедура проілюстрована графічно.
статистично значиме, тобто значно відрізняється від нуля. Більше того, як показано у (6.1.5), отримана за (7.1.1) відповідна p–величина вкрай мала. На рис. 7.1. описана вище процедура проілюстрована графічно.
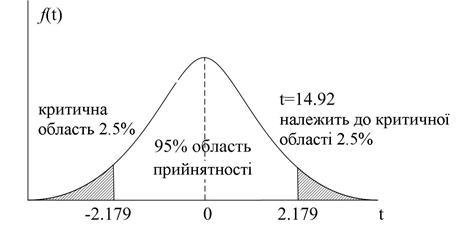
Рис. 7.1.
Раніше ми встановили тісний зв’язок між перевіркою гіпотез і оціненими довірчими інтервалами. Для нашого прикладу 95%-й довірчий інтервал для  визначається нерівністю
визначається нерівністю
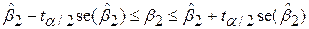 . .
|
Одержуємо
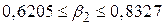
| (7.1.2) |
Таким чином,  лежить між 0,6205 і 0,8327 з 95% вірогідністю. Так, якщо 100 вибірок обсягом 15 одиниць дозволяють побудувати 100 довірчих інтервалів вигляду
лежить між 0,6205 і 0,8327 з 95% вірогідністю. Так, якщо 100 вибірок обсягом 15 одиниць дозволяють побудувати 100 довірчих інтервалів вигляду  , то 95 із них повинні містити істинне значення параметра
, то 95 із них повинні містити істинне значення параметра  . Оскільки значення
. Оскільки значення  , постулюєме нульовою гіпотезою, не потрапляє в інтервал (7.1.2), ми приходимо до висновку про відхилення нульової гіпотези. Це очевидно, враховуючи зв’язок між t-тестом і довірчими інтервалами.
, постулюєме нульовою гіпотезою, не потрапляє в інтервал (7.1.2), ми приходимо до висновку про відхилення нульової гіпотези. Це очевидно, враховуючи зв’язок між t-тестом і довірчими інтервалами.
Дотримуючись аналогічної процедури, ми можемо перевірити й інші гіпотези, що стосуються параметрів моделі (6.4), якщо скористатися результатами регресійного аналізу (6.5). Наприклад, ми можемо відкинути гіпотези про рівність нулю решти коефіцієнтів регресії з a=0,05.
Дата добавления: 2016-07-27; просмотров: 2115;











