Перевірка гіпотез: підхід, оснований на перевірці значимості
Перевірка значимості коефіцієнта регресії: t–тест.
Альтернативний по відношенню до методу довірчого інтервалу, але доповнюючий його метод перевірки статистичних гіпотез, є підхід перевірки на значимість, що розроблявся незалежно Р.А.Фішером (R.A.Fisher) і спільно Нейманом і Пірсоном (Neyman and Pearson). У загальному значенні перевірка на значимість є процедура, за допомогою якої результати вибірки використовуються для перевірки істинності або помилковості нульової гіпотези. Основна мета, що лежить в основі цього, полягає в перевірці статистики (оцінювача) і розподілу вибірки за умови виконання нульової гіпотези. Рішення про те, прийняти або відкинути Н0, приймається на основі величини перевірки статистики, виконаної на даних, що є в розпорядженні .
Як ілюстрацію пригадаємо, що при припущенні про нормальність розподіл змінної
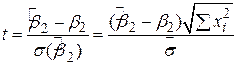 , , 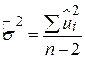
| (3.6.1) |
підпорядковується розподілу Ст’юдента з (N–2) степенями вільності. Якщо істинне значення  визначене нульовою гіпотезою, змінна t може бути легко обчислена за наявними даними вибірки, і, отже, може сприяти перевірці статистики. А оскільки цей тест статистики відповідає t–розподілу, можна записати такий довірчий інтервал:
визначене нульовою гіпотезою, змінна t може бути легко обчислена за наявними даними вибірки, і, отже, може сприяти перевірці статистики. А оскільки цей тест статистики відповідає t–розподілу, можна записати такий довірчий інтервал:
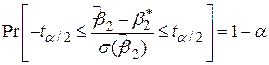 , ,
| (3.6.2) |
де 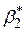 - величина
- величина  за визначенням Н0, а
за визначенням Н0, а 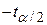 і
і 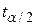 - величини (критичні величини), отримані з таблиці розподілу Ст’юдента для a/2рівня значимості й N–2 степенів вільності.
- величини (критичні величини), отримані з таблиці розподілу Ст’юдента для a/2рівня значимості й N–2 степенів вільності.
Довірчий інтервал, перетворюваний (3.2.7) до вигляду
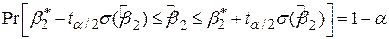 , ,
| (3.6.3) |
дає інтервал, куди 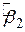 потрапляє з імовірністю 1–a при даному
потрапляє з імовірністю 1–a при даному 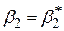 . При перевірці гіпотез 100(1–a)%-й довірчий інтервал (3.2.8) відомий як область прийнятності (region асceptance), а область поза цим довірчим інтервалом називається критичною областю або областю відмови гіпотези. Як було відзначено раніше, самі кінці довірчого інтервалу носять назву критичних величин.
. При перевірці гіпотез 100(1–a)%-й довірчий інтервал (3.2.8) відомий як область прийнятності (region асceptance), а область поза цим довірчим інтервалом називається критичною областю або областю відмови гіпотези. Як було відзначено раніше, самі кінці довірчого інтервалу носять назву критичних величин.
Внутрішній зв’язок між довірчим інтервалом і тестом на перевірку значимості гіпотези можна чіткіше побачити, якщо порівняти (3.6.4) і (3.6.5)
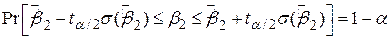 ; ;
| (3.6.4) |
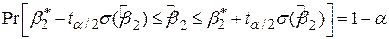 . .
| (3.6.5) |
У процедурі побудови довірчого інтервалу ми намагаємося встановити область або інтервал, у який з певною імовірністю потрапляє істинне значення  , тоді як у тесті на перевірку значимості ми надаємо величині
, тоді як у тесті на перевірку значимості ми надаємо величині  деякого значення і намагаємося визначити, чи лежить підраховане значення
деякого значення і намагаємося визначити, чи лежить підраховане значення 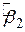 у достатній близькості від прийнятої величини для
у достатній близькості від прийнятої величини для  .
.
Звернемося знову до нашого прикладу “споживання - дохід”. Ми знаємо, що 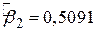 ,
, 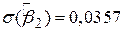 і df = 8. Якщо ми покладемо a=5%
і df = 8. Якщо ми покладемо a=5% 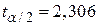 і вважатимемо
і вважатимемо 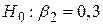 і
і 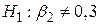 , то з (3.2.8) одержимо
, то з (3.2.8) одержимо
 , ,
| (3.6.6) |
як показано на рис. 3.3.
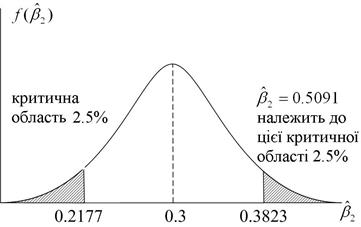
Рис. 3.3. 95%-й довірчий інтервал для  при гіпотезі, що
при гіпотезі, що 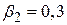
На практиці немає необхідності обчислювати (3.6.3) явно. Можна обчислити величину 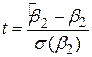 , що стоїть посередині нерівності (3.6.2), і подивитися, чи лежить вона між критичними значеннями t чи ні. Для нашого випадку
, що стоїть посередині нерівності (3.6.2), і подивитися, чи лежить вона між критичними значеннями t чи ні. Для нашого випадку
| t=5,86 | (3.6.7) |
бачимо, що вона лежить у критичній області, зображеній на рис. 3.4.
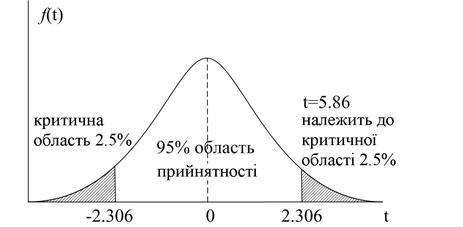
Рис. 3.4. 95%-й довірчий інтервал для t (df = 8)
Зауважимо, що якщо 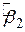 дорівнює значенню, взятому за гіпотезою, то величина t у (3.3.10) буде дорівнювати 0. У міру того як
дорівнює значенню, взятому за гіпотезою, то величина t у (3.3.10) буде дорівнювати 0. У міру того як 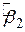 віддалятиметься від значення, взятого за гіпотезою, |t| зростатиме. Отже, “велика величина” |t| служить аргументом проти гіпотези. Звичайно, ми завжди можемо використовувати таблицю розподілу Ст’юдента для визначення того, чи є конкретна величина t великою або малою; відповідь, як ми знаємо, залежить від кількості степенів вільності й від імовірності припустимої помилки. Із таблиці t–розподілу можна побачити, що для будь-якої даної величини df імовірність отримання все більшої величини |t| стає все меншою. Так, для df=20імовірність отримання |t|=1,725 і більше дорівнює 0,10 або 10%, але для тієї ж величини df імовірність отримання |t|=3,552 і більше дорівнює тільки 0,002 або 0,2%.
віддалятиметься від значення, взятого за гіпотезою, |t| зростатиме. Отже, “велика величина” |t| служить аргументом проти гіпотези. Звичайно, ми завжди можемо використовувати таблицю розподілу Ст’юдента для визначення того, чи є конкретна величина t великою або малою; відповідь, як ми знаємо, залежить від кількості степенів вільності й від імовірності припустимої помилки. Із таблиці t–розподілу можна побачити, що для будь-якої даної величини df імовірність отримання все більшої величини |t| стає все меншою. Так, для df=20імовірність отримання |t|=1,725 і більше дорівнює 0,10 або 10%, але для тієї ж величини df імовірність отримання |t|=3,552 і більше дорівнює тільки 0,002 або 0,2%.
Оскільки ми застосовуємо t–розподіл, попередня процедура перевірки має відповідну назву t–тесту. На мові перевірки значимості про статистику говорять, що вона є статистично значимою, якщо величина статистики лежить у критичній області. У такому випадку нульова гіпотеза відкидається. За тих же умов про тест говорять як про статистично не значимий, якщо величина тесту статистики лежить в області прийнятності. У цьому випадку нульова гіпотеза не відкидається. У нашому прикладі t–тест є значимий і, отже, ми відкидаємо нульову гіпотезу.
Перш ніж закінчити обговорення теми перевірки гіпотез, зазначимо, що описана процедура перевірки відома як двостороння процедура перевірки значимості, у якій ми розглядаємо два хвости розподілу імовірності в області відкидання гіпотези і відкидаємо гіпотезу, якщо вона лежить у будь-якому з цих хвостів. Але це сталося через те, що Н1 - двостороння складна гіпотеза;  означає, що
означає, що  більше 0,3 або менше 0,3. Але припустимо, що наш попередній досвід підказує, що МРС повинен бути більше ніж 0,3. У цьому випадку ми маємо:
більше 0,3 або менше 0,3. Але припустимо, що наш попередній досвід підказує, що МРС повинен бути більше ніж 0,3. У цьому випадку ми маємо: 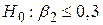 і
і 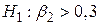 . ХочаН1 залишається складною гіпотезою, зараз вона одностороння. Для перевірки цієї гіпотези ми використовуємо односторонній тест (правосторонній хвіст), як показано на рис. 3.5.
. ХочаН1 залишається складною гіпотезою, зараз вона одностороння. Для перевірки цієї гіпотези ми використовуємо односторонній тест (правосторонній хвіст), як показано на рис. 3.5.
Процедура перевірки залишається тією ж, що й раніше, за винятком того, що верхня критична межа тепер відповідає 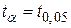 , тобто рівню 5%. Як показано на рис. 3.5, нам не потрібно розглядати ліву частину кривої розподілу в такому випадку. Розгляд односторонньої або двосторонньої області залежить від того, як формулюється альтернативна гіпотеза, що, у свою чергу, залежить від раніше набутого досвіду.
, тобто рівню 5%. Як показано на рис. 3.5, нам не потрібно розглядати ліву частину кривої розподілу в такому випадку. Розгляд односторонньої або двосторонньої області залежить від того, як формулюється альтернативна гіпотеза, що, у свою чергу, залежить від раніше набутого досвіду.


Рис. 3.5. Односторонній тест значимості
Ми можемо підвести підсумки стосовно t–тесту перевірки значимості в табл. 3.1.
Таблиця 3.1
Т–тест значимості: прийняття рішення
| Тип гіпотези | Н0: нульова гіпотеза | Н1: альтернативна гіпотеза | Прийняття рішення: відкинути Н0, якщо |
| Двостороння | 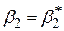
| 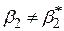
| 
|
| Правостороння | 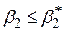
| 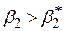
| 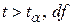
|
| Лівостороння | 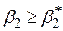
| 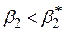
| 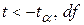
|
3.7. Перевірка значимості 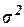 : хі-квадрат тест
: хі-квадрат тест
Як інший приклад застосування методології тесту значимості розглянемо таку змінну
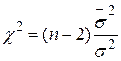 , ,
| (3.7.1) |
яка, як було зазначено раніше, розподіляється за законом розподілу  з (N–2) степенями вільності. Для нашого прикладу
з (N–2) степенями вільності. Для нашого прикладу 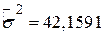 і df = 8. Якщо ми постулюємо, що Н0: s2 = 85;
і df = 8. Якщо ми постулюємо, що Н0: s2 = 85; 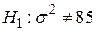 , то рівняння (3.4.1) - перевірка статистики для Н0. Підставляючи в (3.7.1) відповідні значення вхідних величин, одержуємо
, то рівняння (3.4.1) - перевірка статистики для Н0. Підставляючи в (3.7.1) відповідні значення вхідних величин, одержуємо
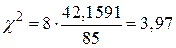 . .
|
Таблиця 3.2
Сумарна таблиця тесту 
| Тип гіпотези | Н0: нульова гіпотеза | Н1: альтернативна гіпотеза | Прийняття рішення: відкинути Н0, якщо |
| Двостороння | 
| 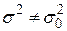
| 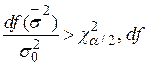 або
або

|
| Правостороння | 
| 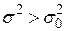
| 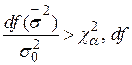
|
| Лівостороння | 
| 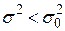
| 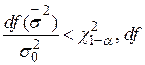
|
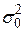 є величина є величина 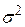 за нульовою гіпотезою за нульовою гіпотезою
|
Якщо ми покладемо a=5%, критичні значення для  будуть 2,1797 і 17,5346. Оскільки підрахована величина
будуть 2,1797 і 17,5346. Оскільки підрахована величина  лежить між цими межами, дані підтримують нульову гіпотезу і ми її не відкидаємо (див. рис. 3.1). Ця процедура перевірки носить назву
лежить між цими межами, дані підтримують нульову гіпотезу і ми її не відкидаємо (див. рис. 3.1). Ця процедура перевірки носить назву  –тесту значимості. У табл. 3.2 наводяться узагальнення
–тесту значимості. У табл. 3.2 наводяться узагальнення  –тесту значимості.
–тесту значимості.
Дата добавления: 2016-07-27; просмотров: 2452;











