ПРИПУЩЕННЯ НОРМАЛЬНОСТІ РОЗПОДІЛУ ЗАЛИШКІВ

Якби нашою єдиною метою було отримання точних оцінок параметрів моделі регресії за МНК, який не вимагає ніяких припущень про закон розподілу залишків, то отриманих результатів було б достатньо. Проте якщо метою дослідження є й отримання статистичних висновків, то нам необхідно зробити припущення про закон розподілу .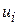

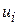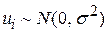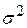З причин, детально розглянутих раніше, ми знову припускаємо, що підпадають під нормальний закон розподілу з нульовим середнім і постійною дисперсією і . При цьому припущенні виявляється, що знайдені за МНК частинні коефіцієнти регресії є найкращими лінійними незміщеними оцінками. Крім того, оцінки 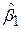, , 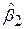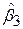самі підкоряються нормальному закону розподілу із середніми значеннями 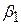, , 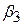і дисперсіями, визначуваними за формулами (5.4.9), (5.4.11) і (5.4.14). Величина 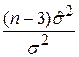підкоряється закону розподілу 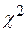з (n–3) степенями вільності, а три оцінки коефіцієнтів регресії розподілено незалежно від 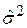. На підставі вищезазначеного можна показати, що замінюючи 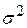на її незміщену оцінку 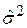у формулах для стандартних похибок, кожна з величин

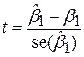;	(6.1)
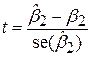;	(6.2)
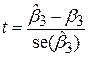
	(6.3)

розподілена за законом t-розподілу з (n–3) степенями вільності.

Відзначимо, що кількість степенів вільності тепер складає (n–3), оскільки для обчислення 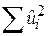і, отже, 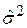нам спочатку необхідно визначити три частинні коефіцієнти регресії. Унаслідок цього на суму квадратів залишків (RSS) накладаються три обмеження (за логікою в моделі з чотирма змінними кількість степенів вільності дорівнює n–4і т.д.).

Таким чином, t-розподіл може бути застосований для побудови довірчих інтервалів, а також для перевірки статистичних гіпотез про значення істинних коефіцієнтів регресії. Аналогічно, розподіл 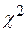може бути використаний для перевірки гіпотез про істинне значення 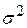. Для демонстрації описаного механізму звернемося до ілюстрованого прикладу.