Перевірка гіпотез про індивідуальні коефіцієнти регресії в матричному позначенні

Якщо нашою метою є проведення статистичних висновків, то нам необхідно припустити, що збурення 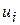підкоряються деякому закону розподілу. Як ми раніше вже згадували, у регресійному аналізі ми звичайно приймаємо, що кожний 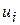підкоряється нормальному закону розподілу з нульовим математичним сподіванням і постійною дисперсією 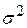. У матричних позначеннях ми запишемо

.

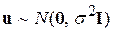(9.6.1)

Припускаючи нормальність розподілу вектора uу разі дво- й тривимірних моделей лінійної регресії, ми знаємо, що отримані за МНК оцінки 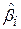також нормально розподілені. Узагальнюючи цей результат на випадок k змінних, можна показати, що

,

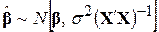тобто кожен елемент вектора 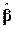розподілений нормально з математичним сподіванням, яке дорівнює відповідному елементу істинного 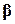, а дисперсія задається добутком 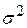на відповідний діагональний елемент оберненої матриці .

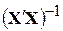Оскільки на практиці 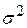невідома, то використовують її оцінку 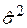. У такому разі шляхом звичайного переходу до t-розподілуприходимо до висновку про те, що кожний елемент вектора 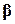підкоряється закону t-розподілуз (n–k) степенями вільності. У математичних позначеннях

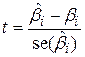
(9.6.2)

з (n–k) степенями вільності, де 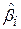– будь-яка компонента вектора 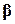. Отже, t-розподілможе бути застосований для перевірки гіпотез про істинне значення 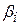, а також встановлення для 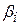довірчого інтервалу. Сам механізм застосування обговорювався нами раніше.