Зв’язок між особистими витратами й особистими доходами в США в 1956 –1970 рр.
Припустимо, що ми хочемо досліджувати зміну особистих витрат в США за декілька минулих років. Скористаємося такою простою моделлю:
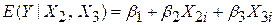 , ,
| (6.4) |
де Y – особисті витрати;
Х2 – особистий дохід (після сплати податків);
Х3 – час, що виміряється в роках.
Рівняння (6.4) постулювало лінійний зв’язок між особистими доходами, доходами і часом або змінною тренда. У більшості випадків множинного регресійного аналізу, що включає дані тимчасових рядів, у модель вводять на додаток до інших пояснювальних змінних змінну тренда, що пояснюється такими причинами.
1. Нас може цікавити, як залежна змінна поводиться зі зміною часу. Наприклад, на графіках часто демонструється, скажімо, поведінка ВНП, зайнятості, безробіття, вартості акцій тощо за деякі послідовні інтервали часу. Вид цих графіків дозволяє визначити тенденцію зміни величини за часом, її зростання, спадання або відсутність певної тенденції. У подібному аналізі нас можуть не цікавити причини, що стоять за тенденцією зростання або спадання досліджуваної величини, а метою може бути просто опис даних, змінюваних у часі.
2. У багатьох випадках змінна тренда є заміною для основної змінної, що впливає на Y. Але ця основна змінна не дозволяє отримати дані, що описують її, або їх отримання пов’язане зі значними труднощами. Наприклад, у моделі виробництва подібною змінною є технологія. Ми чудово розуміємо її вплив, проте незрозуміло, як його виміряти. Отже, можна припустити, що технологія є деяка функція часу, що вимірюється хронологічно. У деяких ситуаціях можна вважати, що впливаюча на Y основна змінна настільки тісно пов’язана з часом, що зручніше ввести в модель сам час, а не цю змінну. Наприклад, у моделі (6.4) час Х3 може представляти населення. Витрати на споживання зростають зі зростанням населення, а саме населення може бути достатньо добре описане лінійною функцією часу.
4. Ще однією підставою для введення змінної тренда є бажання уникнути псевдокореляції. Дані, що стосуються економічних тимчасових рядів, таких як PCE і PDI, часто змінюються в одному напрямі, відображаючи тенденцію зростання або спадання. Отже, якщо побудувати модель регресії PCE по відношенню до PDI, то можна отримати велике значення R2, що може не відображати істинного зв’язку між РСЕ і PDI, а просто бути наслідком загального тренда. Щоб виключити псевдоасоційованість між економічними тимчасовими рядами, можна застосувати кілька прийомів. В одному випадку, припускаючи, що тимчасові ряди демонструють лінійну тенденцію, можна ввести в модель час або саму тенденцію, як це зроблено в рівнянні (6.4). Унаслідок чого  в рівнянні (6.4) відображає істинний зв’язок між РСЕ і PDI. В іншому випадку можна здійснити процедуру детренда Y (PCE) і X2 (PDI), а потім провести регресію за отриманими після детренда змінними Y і X2, припускаючи наявність лінійного етапу, як це було виконано в розд. 5. Спочатку проводимо регресію Y за X3 (час) і одержуємо залишки від цієї регресії, скажімо
в рівнянні (6.4) відображає істинний зв’язок між РСЕ і PDI. В іншому випадку можна здійснити процедуру детренда Y (PCE) і X2 (PDI), а потім провести регресію за отриманими після детренда змінними Y і X2, припускаючи наявність лінійного етапу, як це було виконано в розд. 5. Спочатку проводимо регресію Y за X3 (час) і одержуємо залишки від цієї регресії, скажімо 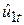 . Потім проводимо регресію X2 за X3 і одержуємо залишки з цієї регресії, наприклад
. Потім проводимо регресію X2 за X3 і одержуємо залишки з цієї регресії, наприклад 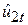 . Нарешті, проводимо регресію
. Нарешті, проводимо регресію 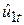 за
за 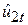 , які не піддаються впливу (лінійному) часу. Кутовий коефіцієнт у цій регресії відображатиме істинний зв’язок між Y і X2 і повинен, отже, дорівнювати коефіцієнту
, які не піддаються впливу (лінійному) часу. Кутовий коефіцієнт у цій регресії відображатиме істинний зв’язок між Y і X2 і повинен, отже, дорівнювати коефіцієнту  . Зрозуміло, що перший метод більш придатний, оскільки він менш трудомісткий.
. Зрозуміло, що перший метод більш придатний, оскільки він менш трудомісткий.
Для перевірки моделі (6.4) скористаємося даними, наведеними в табл. 6.1
Таблиця 6.1
Витрати на споживання і особистий дохід у США за 1956–1970 рр.
| РСЕ, Y, млрд дол. | PDI, X2, млрд дол. | Час, X3 |
| 281,4 | 309,3 | 1956=1 |
| 288,1 | 316,1 | 1957=2 |
| 290,0 | 318,8 | 1958=3 |
| 307,3 | 333,0 | 1959=4 |
| 316,1 | 340,3 | 1960=5 |
| 322,5 | 350,5 | 1961=6 |
| 338,4 | 367,2 | 1962=7 |
| 353,3 | 381,2 | 1963=8 |
| 373,7 | 408,1 | 1964=9 |
| 397,7 | 434,8 | 1965=10 |
| 418,1 | 458,9 | 1966=11 |
| 430,1 | 477,5 | 1967=12 |
| 452,7 | 499,0 | 1968=13 |
| 468,1 | 513,5 | 1969=14 |
| 476,9 | 533,2 | 1970=15 |
Рівняння регресії, отримане за даними табл.6.1, має вигляд
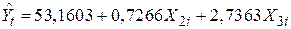 (13,0261) (0,0487) (0,8486)
t = (4,0811) (14,9060) (3,2246)
p = (0,0008) (0,000) (0,0036)
DF=12, R2=0,9988,
(13,0261) (0,0487) (0,8486)
t = (4,0811) (14,9060) (3,2246)
p = (0,0008) (0,000) (0,0036)
DF=12, R2=0,9988, 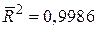 , F2,12=5128,88 , F2,12=5128,88
| (6.5) |
Інтерпретація рівняння (6.5). Якщо обидві змінні Х2 і Х3 перетворюються в нуль, то середня величина витрат на споживання, що, можливо, відображає вплив не включених у модель чинників, приблизно дорівнює 53,16 млрд. дол. Як уже неодноразово наголошувалося величина коефіцієнта 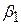 часто не має істотного економічного змісту. Частинний коефіцієнт регресії 0,7266 означає, що при фіксованому значенні решти змінних (Х3 у даному випадку), збільшення особистого доходу на 1 дол. спричиняє зростання особистих витрат на споживання на 73 центи. Аналогічно, якщо не змінювати значення Х2, то за рік особисті витрати на споживання зростають приблизно на 2,7 млрд дол. Значення R2=0,9988 показує високу степінь (близько 99.9%) пояснення двома змінними дисперсії за даний період. Скорегований
часто не має істотного економічного змісту. Частинний коефіцієнт регресії 0,7266 означає, що при фіксованому значенні решти змінних (Х3 у даному випадку), збільшення особистого доходу на 1 дол. спричиняє зростання особистих витрат на споживання на 73 центи. Аналогічно, якщо не змінювати значення Х2, то за рік особисті витрати на споживання зростають приблизно на 2,7 млрд дол. Значення R2=0,9988 показує високу степінь (близько 99.9%) пояснення двома змінними дисперсії за даний період. Скорегований 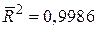 коефіцієнт детермінації демонструє, що після обчислення кількості степенів вільності змінні Х2 і Х3 продовжують пояснювати близько 99,8% дисперсії Y.
коефіцієнт детермінації демонструє, що після обчислення кількості степенів вільності змінні Х2 і Х3 продовжують пояснювати близько 99,8% дисперсії Y.
Дата добавления: 2016-07-27; просмотров: 1941;











