Перевірка гіпотез: загальні зауваження

Обговоривши проблеми точкової і інтервальної оцінок, ми перейдемо до розділу про перевірку гіпотез. Зазначимо коротко деякі загальні аспекти цієї проблеми.

Проблема перевірки статистичних гіпотез може бути сформульована таким чином: узгоджується дане спостереження або висновок з деякою сформульованою гіпотезою чи ні? Використовуваний термін “узгоджуватися” слід розуміти в значенні «достатньої близькості» до величини, про яку йдеться в гіпотезі. Отже, ми не відкидаємо цю гіпотезу. 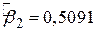Так, якщо деяка теорія або досвід приводить нас до переконання, що істинне значення кутового коефіцієнта в прикладі “споживання - дохід”, є одиниця, чи є , отримане з розрахунків за даними з вибірки в табл. 1.3. Якщо це так, ми не відкидаємо гіпотезу, інакше ми можемо її відкинути.

Мовою статистики зазначена гіпотеза має назву нульової гіпотези і позначається символом Н₀. Нульова гіпотеза перевіряється альтернативною гіпотезою Н₁ (відомою також як maintained hypothesis), яка може стверджувати, наприклад, що істинне не дорівнює одиниці. Альтернативна гіпотеза може бути простою або складною (composite). Наприклад, Н₁: 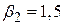є проста гіпотеза, а Н₁: 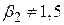- складна гіпотеза.

Теорія перевірки гіпотез займається розвитком методів або процедур для вирішення питання стосовно нульової гіпотези. Існує два взаємно доповнювальних підходи для розробки (devising) таких правил: довірчий інтервал і перевірка значимості. Згідно з цими підходами, дана змінна (статистика або оцінювач) має деякий розподіл імовірності й перевірка гіпотез включає висловлювання про величини параметрів таких розподілів. Наприклад, ми знаємо, що при припущенні про нормальний розподіл 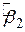має математичне сподівання і дисперсію, визначувану (2.3.3). Якщо ми висуваємо гіпотезу, що 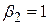, ми робимо припущення про один з параметрів нормального розподілу, а саме, про його математичне сподівання. Більшість із тих статистичних гіпотез, що розглядатимуться нами далі, будуть подібного типу – висловлювання припущення про один або більше параметрів розподілів, таких як нормальний, F, t або . Як це відбувається на практиці розглянемо у двох наступних підрозділах.