Задача розподілу потоків

Ця задача відноситься до задач другого і четвертого типів, постановка яких наведена в розділі 3.1. В цьому розділі розглядається задача розподілу потоків, в якій вважається, що пропускні спроможності задані, а потоки потрібно розподілити так, щоб мінімізувати середнє значення часу перебування в мережі 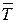– задача другого типу.

В цьому випадку може виникнути ситуація, коли потік по маршруту 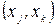перевищує пропускну спроможність каналу, тобто 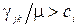. Ця ситуація вимагає розщеплення одного потоку по кількох каналах.

Розв’язок цієї задачі базується на теоремі Форда-Фалкерсона та угорському алгоритмі.

З рівності (3.4) маємо

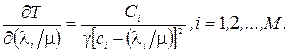
Звідси видно, що

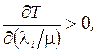
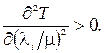
Отже, можна зробити висновки, що Т – опукла функція потоків і має мінімум.

Не вдаючись в подробиці виводу (тих хто цікавиться відсилаємо до [28, 29]) сформулюємо алгоритм розв’язку задачі методом відхилення потоку.

КРОК 1. Покласти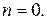

КРОК 2. Для кожного і = 1, 2, ..., М знайти довжину

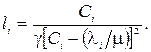
КРОК 3. Знайти 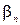– добав очний вартісний коефіцієнт для цього потоку

.

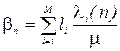КРОК 4. Розв’язати задачу відшукання потоків по найкоротшому маршруту (розділ 2.1.). Позначимо вектор потоків

.

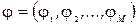КРОК 5. Знайти 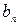– добавлений вартісний коефіцієнт для потоку по найкоротшому маршруту

.

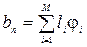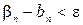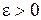КРОК 6. (Правило зупинки). Якщо , де – допуск, то зупинка. Якщо ні, то перехід на крок 7.

КРОК 7. Знайти таке значення 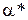, , 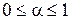для якого потік 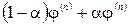мінімізує Т. Це можна зробити любим методом пошуку, наприклад методом Фібоначчі.

КРОК 8. Покласти

.

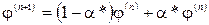КРОК 9. Покласти 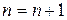. Перейти до кроку 2.

Тих, хто більш детально цікавиться алгоритмами відшукання оптимального розподілу потоків, відсилаємо до / /.