Поліноміальная модель регресії

Розглянемо так званий клас поліноміальних моделей регресії, що широко застосовуються в дослідженнях, пов’язаних із функцією виробництва. Беручи до розгляду ці моделі, ми ще більше розширюємо область застосування класичної лінійної моделі регресії.

Для кращого розуміння суті розглянемо рис. 5.3, який демонструє зв’язок короткострокових граничних витрат Y на виробництво продукції і обсяг виробництва Х. Схематично побудована крива витрат має U-подібний вигляд, що свідчить про нелінійність зв’язку граничних витрат і обсягу виробництва. У зв’язку з цим виникає питання про вибір економетричної моделі, яка правильно б відображала первинне зниження та подальше зростання граничних витрат.

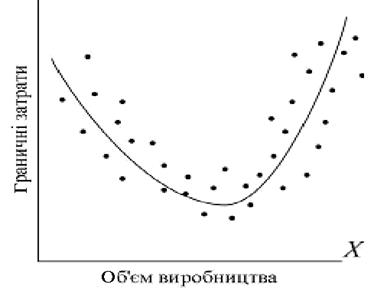
Рис. 5.3. Крива граничних витрат

Зображена на рис. 5.3 крива формою нагадує параболу. Рівняння параболи має вигляд

.

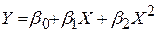(5.10.1)

Стохастичний аналог цього рівняння

.

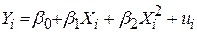(5.10.2)

Дане рівняння має назву поліноміальної регресії 2-го порядку.

У загальному випадку поліноміальна регресія k-го порядку може бути записана у вигляді

.

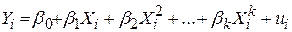(5.10.3)

Відзначимо, що цей тип регресії має тільки одну пояснювальну змінну, яка входить в рівняння з різними степенями. Унаслідок цього ми маємо множинну регресію.

Чи має ця модель які-небудь особливості в порівнянні з раніше розглянутими? Оскільки коефіцієнти регресії входять в моделі (5.10.2), (5.10.3) лінійно, до них може бути застосований звичайний метод найменших квадратів. Чи виникає при цьому проблема мультиколінеарності? Чи можуть бути висококорельованими різні степені Х? Якщо пригадати, що Х₂, Х₃ і так далі є лінійними функціями, то мультиколінеарність поліноміальній регресії не загрожує.

Для прикладу поліноміальної регресії звернемося до даних із виробництва товару та загальних витрат на його виробництво, наведених у табл. 5.3.

Таблиця 5.3

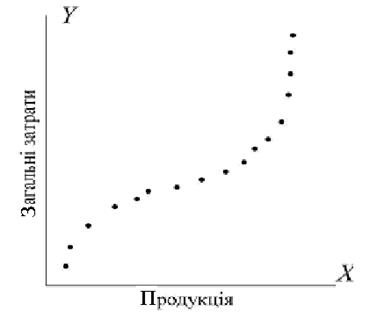
Рис. 5.4

Щоб визначити тип регресії, який відповідає даним табл.5.3, слід зобразити ці дані на площині. З поданого графіка (рис.5.4) бачимо, що співвідношення між випуском продукції та загальними витратами на виробництво має вигляд, подібний до букви S. Для опису залежності, яка нас цікавить, зручною є поліноміальна регресія третьої степені

,

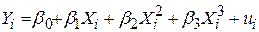де Y – загальні витрати, а X – продукція.

Застосувавши цю модель для наведених у таблиці даних, отримаємо рівняння

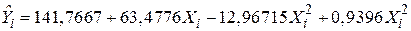(6,3753) (4,7786) (0,9857) (0,0591) R2=0,9983.

У дужках вказані стандартні похибки коефіцієнтів регресії.

Висновки

1. Термін лінійна модель множинної регресії стосується поняття лінійності за коефіцієнтами регресії.

2. Хоча модель регресії з трьома змінними багато в чому є продовженням двовимірної моделі, з’являються й нові поняття, такі як “частинні коефіцієнти регресії”, “частинні коефіцієнти кореляції”, “множинний коефіцієнт кореляції”, “скорегований і нескорегований коефіцієнти детермінації”, “мультиколінеарність”.

3. Хоча і є сукупною мірою якості підгонки регресії до початкових даних, їх значущість не слід перебільшувати. Критичними є такі чинники, як відповідність знаків коефіцієнтів моделі нашим апріорним уявленням, а також їх статистична значущість.

4. Наведені результати для моделі з трьома змінними можна узагальнити на випадок лінійної моделі регресії, що містить будь-яку кількість регресорів. Однак при цьому алгебраїчні вирази стають дуже громіздкими. Цей недолік долається шляхом переходу до матричних операцій.