Виробнича функція Коба – Дугласа
У попередньому розділі ми показали, як шляхом відповідного перетворення можна перейти від нелінійного за змінними рівняння до лінійного з подальшою реалізацією схеми регресійного аналізу. Цей прийом може бути застосований і в моделях з кількістю змінних, більшою за двох. Покажемо це на прикладі відомої виробничої функції Коба – Дугласа.
Функція Коба – Дугласа може бути подана в статистичній формі таким чином:
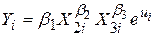 , ,
| (5.9.1) |
де 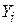 – вироблена продукція; X2i – трудовитрати; X3i – капіталозатрати, ui – стохастичний збурюючий складова.
– вироблена продукція; X2i – трудовитрати; X3i – капіталозатрати, ui – стохастичний збурюючий складова.
Рівняння (5.9.1) є нелінійним стосовно змінних, що входять до нього. Після логарифмування (5.9.1) ми одержимо
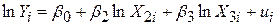 , ,
| (5.9.2) |
де 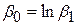 .
.
Така форма рівняння вже є лінійною щодо параметрів 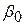 ,
,  ,
, 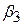 . Зазначимо також, що це рівняння залишається нелінійним стосовно змінних Y, X2, X3, але лінійним за змінними
. Зазначимо також, що це рівняння залишається нелінійним стосовно змінних Y, X2, X3, але лінійним за змінними 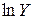 ,
, 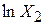 ,
, 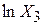 . Ця модель називається «логарифмічною лінійною моделлю». Її двовимірний аналог був нами досліджений на прикладі (6.4.3).
. Ця модель називається «логарифмічною лінійною моделлю». Її двовимірний аналог був нами досліджений на прикладі (6.4.3).
Функція Коба – Дугласа має такі особливості:
1. Коефіцієнт  є частинним коефіцієнтом еластичності виробленої продукції щодо трудовитрат, тобто він є мірою процентної зміни вироблюваної продукції при 1%-му збільшенні, скажімо, трудовитрат і збереженні при цьому на постійному рівні капіталозатрат.
є частинним коефіцієнтом еластичності виробленої продукції щодо трудовитрат, тобто він є мірою процентної зміни вироблюваної продукції при 1%-му збільшенні, скажімо, трудовитрат і збереженні при цьому на постійному рівні капіталозатрат.
2. Коефіцієнт 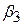 також є частинним коефіцієнтом еластичності виробленої продукції щодо капіталозатрат при постійному рівні трудовитрат.
також є частинним коефіцієнтом еластичності виробленої продукції щодо капіталозатрат при постійному рівні трудовитрат.
3. Сума  +
+ 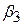 дає інформацію про обсяг збільшення виробництва, тобто являє собою відповідь виробництва на пропорційну зміну витрат. Якщо ця сума дорівнює 1, то ми маємо одиничний обсяг збільшення виробництва, тобто подвоєння витрат викликає подвоєння продукції, потроєння витрат – потрійне збільшення виробництва й т.д. Якщо сума менше 1, ми маємо спадний обсяг виробництва, тобто подвоєння витрат дає менший ніж у два рази приріст виробництва. Нарешті, якщо сума більше 1, ми маємо випадок зростаючого обсягу – подвоєння витрат приводить до збільшення виробництва більше ніж у два рази.
дає інформацію про обсяг збільшення виробництва, тобто являє собою відповідь виробництва на пропорційну зміну витрат. Якщо ця сума дорівнює 1, то ми маємо одиничний обсяг збільшення виробництва, тобто подвоєння витрат викликає подвоєння продукції, потроєння витрат – потрійне збільшення виробництва й т.д. Якщо сума менше 1, ми маємо спадний обсяг виробництва, тобто подвоєння витрат дає менший ніж у два рази приріст виробництва. Нарешті, якщо сума більше 1, ми маємо випадок зростаючого обсягу – подвоєння витрат приводить до збільшення виробництва більше ніж у два рази.
Побіжно відзначимо, що якщо використовується логарифмічна лінійна модель з довільною кількістю змінних, то коефіцієнт при кожній змінній Х є мірою частинної еластичності залежної змінної Y стосовно X. Для моделі з k змінними
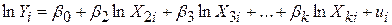 . .
| (5.9.3) |
Кожний коефіцієнт регресії є еластичністю Y щодо відповідної змінної.
Застосуємо виробничу функцію для аналізу агросектору Тайваню за 1958–1972 рр. (табл. 5.2).
Вважаючи, що модель (5.9.2) задовольняє припущення лінійної регресійної моделі, одержуємо
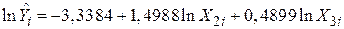 (2,4495) (0,5398) (0,1020)
t = (–1,3629) (2,7765) (4,8005)
(2,4495) (0,5398) (0,1020)
t = (–1,3629) (2,7765) (4,8005)
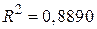 , DF=12; , DF=12;
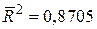 . .
| (5.9.4) |
Таблиця 5.2
Показники агросектору Тайваню в 1958–1972 рр.
| Рік | Валовий продукт Y, млн дол. | Трудодні X2, млн | Капіталозатрати Х3, млн дол. |
| 16607,7 | 275,5 | 17803,7 | |
| 17511,3 | 274,4 | 18096,8 | |
| 20171,2 | 269,7 | 18271,8 | |
| 20932,9 | 267,0 | 19167,3 | |
| 20406,0 | 267,8 | 19647,6 | |
| 20831,6 | 275,0 | 20803,5 | |
| 24806,3 | 283,0 | 22076,6 | |
| 26465,8 | 300,7 | 23445,2 | |
| 27403,0 | 307,5 | 24939,0 | |
| 28628,7 | 303,7 | 26713,7 | |
| 29904,5 | 304,7 | 29957,8 | |
| 27508,2 | 298,6 | 31585,9 | |
| 29035,5 | 295,5 | 33474,5 | |
| 19281,5 | 299,0 | 34821,8 | |
| 31535,8 | 288,1 | 41794,3 |
Таким чином, отримуємо, що в агросекторі Тайваню за період 1958–1972 рр. коефіцієнт еластичності продукції по трудо- і капітало-витратам складав 1,4988 і 0,4899 відповідно. Іншими словами, за досліджуваний період при постійних капіталозатратах збільшення на 1% трудовитрат приводило в середньому до 1,5% зростання виробництва продукції. Аналогічно, при постійних трудовитратах збільшення на 1% капіталозатрат викликало приблизно 0,5% приросту продукції. Складаючи коефіцієнти еластичності виробництва продукції, одержуємо 1,9887, що дає міру обсягу приросту виробництва. Як ми бачимо, за досліджуваний період агросектор Тайваню мав зростаючий обсяг приросту виробництва.
Ми також бачимо, що побудована модель має достатньо високий коефіцієнт детермінації 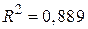 , тобто близько 89% варіації логарифма продукції, яка випускається, пояснюється за рахунок варіації логарифмів трудовитрат і капіталозатрат.
, тобто близько 89% варіації логарифма продукції, яка випускається, пояснюється за рахунок варіації логарифмів трудовитрат і капіталозатрат.
Дата добавления: 2016-07-27; просмотров: 2499;











