Властивості оцінювачів за МНК: теорія Гаусса-Маркова
Як було відзначено раніше, оцінювачі, отримані за МНК при зроблених припущеннях CLRM, мають деякі ідеальні або оптимальні властивості. Вони зазначені в добре відомій теоремі Гаусса-Маркова. Для того щоб зрозуміти її значення, необхідно розглянути властивість найкращого лінійного незміщеного оцінювача (best linear unbiasedness property an estimator). Оцінювач, скажімо 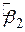 за МНК, вважається найкращим лінійним незміщеним оцінювачем BLUE (best linear unbiased estimator)
за МНК, вважається найкращим лінійним незміщеним оцінювачем BLUE (best linear unbiased estimator) 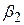 , якщо він має такі властивості:
, якщо він має такі властивості:
1. Він лінійний, тобто являє собою лінійну функцію випадкової змінної, таку як залежна змінна Y в регресійній моделі.
2. Він є незміщеним оцінювачем, тобто 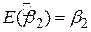 .
.
3. Він має найменшу дисперсію в класі всіх лінійних незміщених оцінювачів; незміщений оцінювач з найменшою дисперсією відомий як ефективний оцінювач.
Можна довести, що оцінювачі, отримані за МНК, мають властивості найкращого лінійного незміщеного оцінювача BLUE. Це є висновком відомої теореми Гаусса-Маркова, яка може бути сформульована таким чином: при прийнятих гіпотезах класичної регресійної лінійної моделі отримані за методом найменших квадратів оцінювачі в класі лінійних незміщених оцінювачів мають найменшу дисперсію, тобто вони є найкращими лінійними незміщеними оцінювачами.
Дана теорема дуже важлива при регресійному аналізі, оскільки стосується як теорії, так і практики.
Пояснимо значення теореми за допомогою рис. 2.10.
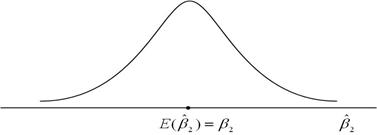
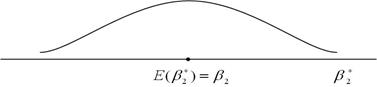
На рис. 2.10, а показаний розподіл за вибірками оцінювача 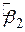 , отриманого за МНК, у вибірках, що повторюються. Для зручності ми припустимо, що розподіл
, отриманого за МНК, у вибірках, що повторюються. Для зручності ми припустимо, що розподіл 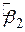 розташований симетрично. Як бачимо з рисунка,математичне сподівання
розташований симетрично. Як бачимо з рисунка,математичне сподівання 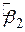 дорівнює істинному значенню
дорівнює істинному значенню 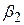 , тобто
, тобто 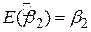 . Це і є значення, яке ми вкладаємо в термін “незміщена оцінка”. На рис. 2.10, б показаний розподіл оцінювача
. Це і є значення, яке ми вкладаємо в термін “незміщена оцінка”. На рис. 2.10, б показаний розподіл оцінювача 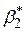 , отриманого за альтернативним методом. Для зручності ми припустили, що
, отриманого за альтернативним методом. Для зручності ми припустили, що 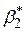 , як і
, як і 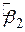 , має властивість незміщеності. Припустимо, що і
, має властивість незміщеності. Припустимо, що і 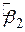 і
і 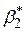 є лінійними оцінювачами, тобто вони є лінійними функціями від Y. Який із оцінювачів -
є лінійними оцінювачами, тобто вони є лінійними функціями від Y. Який із оцінювачів - 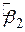 або
або 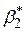 - слід вибрати?
- слід вибрати?
а
б
в
Рис. 2.10. Розподіл за вибіркою за МНК 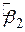 і альтернативного оцінювача
і альтернативного оцінювача 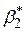 : а - розподіл
: а - розподіл 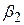 ; б - розподіл
; б - розподіл 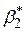 ; в - розподіл
; в - розподіл 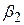 і
і 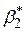
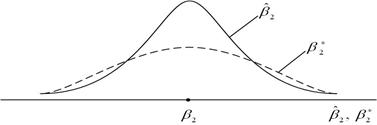
Щоб відповісти на це запитання накладемо два рисунки, як показано на рис. 2.8, в. Із рис. 2.10, в бачимо, що хоча обидва розподіли незміщені, для 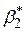 ми маємо більш розмитий розподіл біля середнього значення в порівнянні з розподілом
ми маємо більш розмитий розподіл біля середнього значення в порівнянні з розподілом 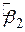 . Іншими словами, дисперсія
. Іншими словами, дисперсія 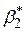 більша, ніж дисперсія
більша, ніж дисперсія 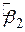 . Зрозуміло, що з двох даних оцінювачів, які мають властивості лінійності і незміщеності, слід вибрати оцінювач із меншою дисперсією, оскільки він ближче до
. Зрозуміло, що з двох даних оцінювачів, які мають властивості лінійності і незміщеності, слід вибрати оцінювач із меншою дисперсією, оскільки він ближче до 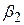 , ніж альтернативний оцінювач. Отже, завжди слід вибирати найкращий лінійний незміщений оцінювач (BLUE).
, ніж альтернативний оцінювач. Отже, завжди слід вибирати найкращий лінійний незміщений оцінювач (BLUE).
Розглянуті нами статистичні властивості відомі як властивості кінцевих вибірок. Ці властивості зберігаються незалежно від розміру вибірки, за даними якої отримані оцінювачі. Пізніше ми матимемо нагоду розглянути асимптотичні властивості, тобто властивості, які зберігаються тільки у випадку, коли вибірка дуже велика (нескінченна).
2.5. Коефіцієнт детермінації 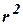 : міра «якості підгонки»
: міра «якості підгонки»
Звернемося зараз до розгляду питання якості підгонки лінії регресії до множини даних, тобто дослідимо, наскільки «добре» лінія вибіркової регресії підходить до цих даних. Із рис.1.1 бачимо, що якби всі спостереження знаходилися на лінії регресії, ми отримали б “точну підгонку”, але на практиці це окремий випадок. У загальному ж випадку будуть як позитивні відхилення 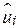 , так і негативні. Ми прагнемо, щоб ці залишки були наскільки можливо малі. Коефіцієнт детермінації
, так і негативні. Ми прагнемо, щоб ці залишки були наскільки можливо малі. Коефіцієнт детермінації  (випадок двох змінних) або
(випадок двох змінних) або 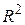 (множинна регресія) являє собою сумарну міру якості підгонки лінії регресії до даних спостереження.
(множинна регресія) являє собою сумарну міру якості підгонки лінії регресії до даних спостереження.
Перш ніж з’ясовувати, як підраховується  , розглянемо евристичне пояснення
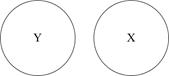
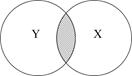
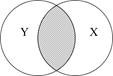
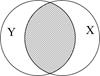
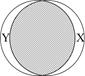
, розглянемо евристичне пояснення  за допомогою графічних діаграм, відомих як діаграма Венна (Venn) (рис. 2.11).
за допомогою графічних діаграм, відомих як діаграма Венна (Venn) (рис. 2.11).
а б в

г д е
Рис. 2.11. Діаграма для пояснення  : а -
: а -  дорівнює 0; б -
дорівнює 0; б -  близький до 0;
близький до 0;
в -  близький до 0,5; г -
близький до 0,5; г -  більш ніж 0,5; д -
більш ніж 0,5; д -  близький до 1;
близький до 1;
е -  дорівнює 1
дорівнює 1
На цій діаграмі коло Y зображає дисперсію залежної змінної Y, а коло Х - дисперсію пояснювальної змінної Х. Перетин двох кіл (заштрихована область) являє собою область, у якій дисперсія Y пояснюється дисперсією в Х (скажімо, за регресією МНК). Чим більша область перетину, тим більше дисперсія Y пояснюєтьсяза допомогою Х. Коефіцієнт детермінації  зображає числову міру області перетину. На рис. 2.9 бачимо, що при русі зліва направо область перекриття збільшується, тобто послідовно зростає частина варіації Y, з’ясована за допомогою Х, -
зображає числову міру області перетину. На рис. 2.9 бачимо, що при русі зліва направо область перекриття збільшується, тобто послідовно зростає частина варіації Y, з’ясована за допомогою Х, -  зростає. Коли перекриття немає,
зростає. Коли перекриття немає,  , очевидно, дорівнює нулю, а коли відбувається повне перекриття, то
, очевидно, дорівнює нулю, а коли відбувається повне перекриття, то 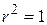 , оскільки 100% дисперсії Y пояснюється за допомогою Х. Як незабаром переконаємося
, оскільки 100% дисперсії Y пояснюється за допомогою Х. Як незабаром переконаємося  лежить між 0 і 1.
лежить між 0 і 1.
Для обчислення коефіцієнта  зробимо так. Пригадаємо, що
зробимо так. Пригадаємо, що
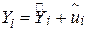
|
або у формі відхилень
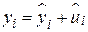 . .
| (2.5.1) |
Підносячи обидві частини цієї рівності у квадрат і підсумовуючи, отримаємо
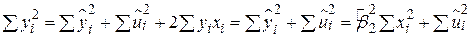 , ,
| (2.5.2) |
оскільки 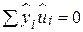 і
і 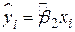 .
.
Різні суми квадратів, що входять у (2.5.2), можуть бути описані таким чином: 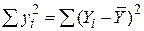 – загальна дисперсія величини Y відносно середньої величини за вибіркою, що називається загальною сумою квадратів TSS (total sum squares);
– загальна дисперсія величини Y відносно середньої величини за вибіркою, що називається загальною сумою квадратів TSS (total sum squares); 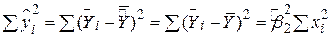 – дисперсія оціненої величини Y щодо її середнього значення ((
– дисперсія оціненої величини Y щодо її середнього значення (( 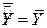 ) або з’ясована сума квадратів з рівняння регресії ESS (explained sum squares);
) або з’ясована сума квадратів з рівняння регресії ESS (explained sum squares); 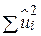 – залишкова або нез’ясована дисперсія величини Y щодо лінії регресії або просто залишкова сума квадратів RSS (residual sum squares). Таким чином, з (2.5.2) одержуємо рівність
– залишкова або нез’ясована дисперсія величини Y щодо лінії регресії або просто залишкова сума квадратів RSS (residual sum squares). Таким чином, з (2.5.2) одержуємо рівність
| TSS=ESS+RSS. | (2.5.3) |
Вона показує, що загальна варіація спостережуваних величин Y щодо їх середнього значення може бути розбита на дві частини, одна відповідає лінії регресії, а інша - випадковим відхиленням, оскільки не всі спостережувані Y лежать на лінії регресії. На рис. 2.10 це розбиття пояснене геометрично.
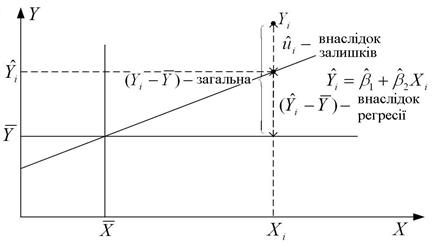
Рис. 2.12. Розбиття варіації 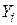 на дві компоненти
на дві компоненти
Розділивши обидві частини (2.5.3) на TSS, одержуємо
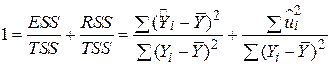 . .
| (2.5.4) |
Визначимо тепер коефіцієнт детермінації 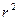 таким способом:
таким способом:
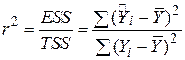
| (2.5.5) |
або в альтернативному вигляді
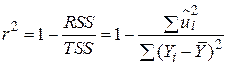 . .
| (2.5.5а) |
Визначена таким чином величина 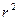 , відома як коефіцієнт детермінації, і є мірою якості підгонки лінії регресії, що широко застосовується.
, відома як коефіцієнт детермінації, і є мірою якості підгонки лінії регресії, що широко застосовується.
Відзначимо такі дві властивості  :
:
1. Коефіцієнт 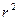 не негативний (випливає з виразу (2.5.5)).
не негативний (випливає з виразу (2.5.5)).
2. 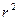 має межі
має межі 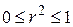 . При значенні
. При значенні 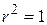 ми маємо випадок точної підгонки, тобто
ми маємо випадок точної підгонки, тобто 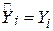 для кожного i. Водночас випадок
для кожного i. Водночас випадок 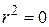 означає відсутність зв’язку між регресантом і регресором (тобто
означає відсутність зв’язку між регресантом і регресором (тобто 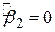 ,
, 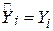 для всіх i). У цьому випадку, як бачимо з рівняння
для всіх i). У цьому випадку, як бачимо з рівняння 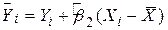 ,
, 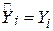 , тобто кращим прогнозом для будь-якої величини Y є її середнє значення. При цьому лінія регресії - паралель осі X.
, тобто кращим прогнозом для будь-якої величини Y є її середнє значення. При цьому лінія регресії - паралель осі X.
Хоча  можна обчислити безпосередньо за формулами (2.5.5), (2.5.5а), простіше скористатися такими формулами:
можна обчислити безпосередньо за формулами (2.5.5), (2.5.5а), простіше скористатися такими формулами:
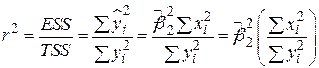 . .
| (2.5.6) |
Розділивши чисельник і знаменник (2.5.6) на розмір вибірки N (або N–1, якщо розмір вибірки малий), одержуємо
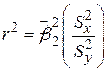 , ,
| (2.5.7) |
де 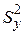 і
і 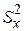 - вибіркові дисперсії (sample variances) за Y і Х відповідно.
- вибіркові дисперсії (sample variances) за Y і Х відповідно.
Оскільки 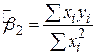 , рівняння (2.5.6) можна зобразити у вигляді
, рівняння (2.5.6) можна зобразити у вигляді
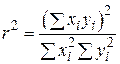 . .
| (2.5.8) |
Застосовуючи вирази для  , ми можемо подати ESS і RSS таким чином:
, ми можемо подати ESS і RSS таким чином:
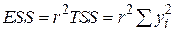 , ,
| (2.5.9) |
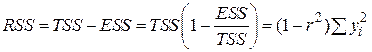 . .
| (2.5.10) |
Отже, ми можемо записати
| TSS=ESS+RSS, | |
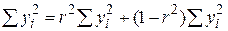 . .
| (2.5.11) |
Коефіцієнт кореляції, що являє собою ступінь асоціативності між двома змінними, кількісно близько пов’язаний з  , але концептуально вони дуже різні. Коефіцієнт кореляції можна визначити за формулою
, але концептуально вони дуже різні. Коефіцієнт кореляції можна визначити за формулою
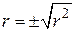
| (2.5.12) |
або
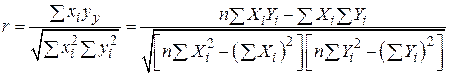 . .
| (2.5.13) |
Визначена таким чином величина має назву коефіцієнта кореляції за вибіркою.
Ось деякі його властивості:
1. Він може бути позитивним або негативним, знак r залежить від знака чисельника (2.5.13), що є мірою коваріації за вибіркою двох змінних.
2. Він лежить між –1 і 1, тобто 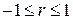 .
.
3. За своєю природою він симетричний, тобто коефіцієнт кореляції між Х і Y (rXY) той же, що й між Y і Х (rYX).
4. Він незалежний по відношенню до вибору початку системи координат і масштабу вздовж осей координат, тобто, якщо ми визначимо 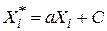 і
і 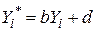 , де
, де 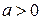 ,
, 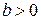 , а, b і d – константи, то r між Х* і Y* те ж, що й між початковими змінними Х і Y.
, а, b і d – константи, то r між Х* і Y* те ж, що й між початковими змінними Х і Y.
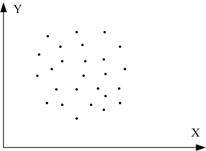
5. Якщо Х і Y статистично незалежні, коефіцієнт кореляції між ними дорівнює нулю, але якщо 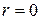 , це не означає, що дві змінні незалежні. Іншими словами, нульовий коефіцієнт кореляції не обов’язково означає незалежність (рис. 2.13з).
, це не означає, що дві змінні незалежні. Іншими словами, нульовий коефіцієнт кореляції не обов’язково означає незалежність (рис. 2.13з).
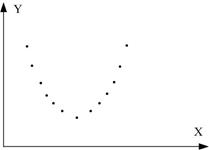
6. Коефіцієнт кореляції є міра тільки лінійної асоціативності або лінійної залежності; він незастосовний для опису нелінійної залежності. Так, на рис. 2.13, з Y=X2 є точна залежність, хоча 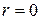 .
.

а б в


г д е
ж з
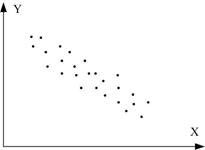
Рис. 2.13. Кореляційний коефіцієнт для різних випадків вибірок:
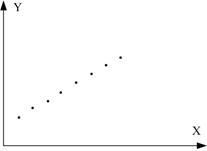
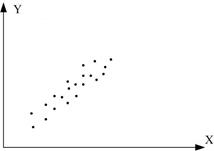
а - r=1; б - r=-1; в - r близький до 1; г - r близький до –1;
д - r додатній, близький до 0; е - r від’ємний, близький до 0; ж - r=0; з - r=0
7. Хоча r є мірою лінійної асоціативності між двома змінними, це необов’язково означає який-небудь причинно-наслідковий зв’язок, як було відзначено раніше.
У контексті регресії  більш інформативний, ніж r, оскільки
більш інформативний, ніж r, оскільки  вказує на частку варіації в залежній змінній, що з’ясовується пояснювальною змінною.
вказує на частку варіації в залежній змінній, що з’ясовується пояснювальною змінною.
Насамкінець зауважимо, що коефіцієнт детермінації  може бути обчислений як квадрат коефіцієнта кореляції між змінними
може бути обчислений як квадрат коефіцієнта кореляції між змінними 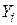 і
і 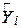 за такою формулою:
за такою формулою:
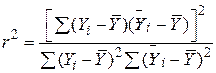
| |
або
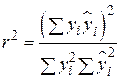 . .
|
Числовий приклад
Проілюструємо теорію економічного аналізу на прикладі функції споживання Кейнса. Пригадаємо, за Кейнсом, “фундаментальним психологічним законом є те, що чоловіки (жінки) налаштовані, як правило, в середньому, збільшувати обсяг споживаних благ у міру зростання свого доходу, але в меншій мірі, ніж збільшується дохід, тобто гранична схильність до споживання (MPC) більше нуля, але менше одиниці”. Хоча Кейнс не вказує точний вид функціональної залежності між споживанням і доходом, для простоти припустимо, що співвідношення лінійне
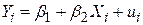 . .
|
Для перевірки теорії Кейнса скористаємося даними вибірки, наведеними в табл. 1.3. Оцінка лінії регресії (рис. 2.14), отже, має вигляд
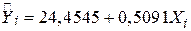 . .
|
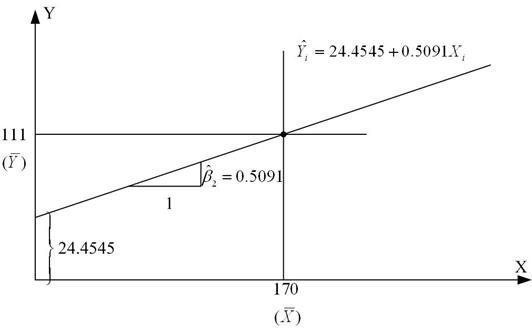
Рис. 2.14. Лінія вибіркової регресії
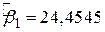 , , 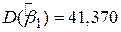 , , 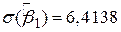 , ,
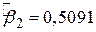 , , 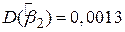 , , 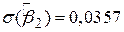 , ,
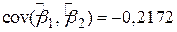 , , 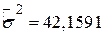 , ,
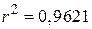 , , 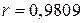 , , 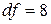 . .
| (2.6.1) |
Оцінена лінія регресії має такий вигляд:
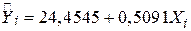 . .
| (2.6.2) |
Відповідно до висловленого вище отримані результати можна інтерпретувати таким чином. Кожна точка на лінії регресії являє собою оцінку очікуваної або середньої величини Y, відповідної вибраному значенню Х; тобто 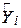 - оцінка
- оцінка 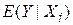 . Величина
. Величина 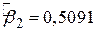 , визначаюча кутовий коефіцієнт лінії регресії показує, що для вибірки з областю зміни Х доходу за місяць між 80 дол. і 260 дол. зі зростанням Х на 1 дол. оцінка збільшення середніх витрат сім’ї на споживання складає близько 51 цента. Величина
, визначаюча кутовий коефіцієнт лінії регресії показує, що для вибірки з областю зміни Х доходу за місяць між 80 дол. і 260 дол. зі зростанням Х на 1 дол. оцінка збільшення середніх витрат сім’ї на споживання складає близько 51 цента. Величина 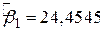 , визначаюча точку перетину лінії регресії з віссю Y, означає середні граничні витрати сім’ї, що має нульовий рівень доходів. Звичайно, це суто механічна інтерпретація коефіцієнта
, визначаюча точку перетину лінії регресії з віссю Y, означає середні граничні витрати сім’ї, що має нульовий рівень доходів. Звичайно, це суто механічна інтерпретація коефіцієнта 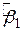 . У регресійному аналізі подібна інтерпретація не завжди відповідає значенню задачі, хоча в нашому прикладі на користь подібного трактування можна сказати, що сім’я без доходу (через безробіття, скорочення виробництва та под.) може підтримувати деякий мінімальний рівень споживання або за рахунок позичання грошей, або використовуючи заощадження. Але в загальному випадку при інтерпретації значення коефіцієнта
. У регресійному аналізі подібна інтерпретація не завжди відповідає значенню задачі, хоча в нашому прикладі на користь подібного трактування можна сказати, що сім’я без доходу (через безробіття, скорочення виробництва та под.) може підтримувати деякий мінімальний рівень споживання або за рахунок позичання грошей, або використовуючи заощадження. Але в загальному випадку при інтерпретації значення коефіцієнта 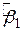 потрібно керуватися здоровим глуздом, оскільки часто область зміни Х може не включати нуль як одну зі спостережуваних величин.
потрібно керуватися здоровим глуздом, оскільки часто область зміни Х може не включати нуль як одну зі спостережуваних величин.
Можливо, краще інтерпретувати 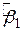 як середню величину впливу на Y всіх змінних, не включених явно в модель. Величина
як середню величину впливу на Y всіх змінних, не включених явно в модель. Величина 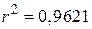 означає, що близько 96% дисперсії тижневих витрат на споживання пояснюється за рахунок доходу. Оскільки
означає, що близько 96% дисперсії тижневих витрат на споживання пояснюється за рахунок доходу. Оскільки 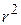 може набути найбільшого значення 1, то можна сказати, що якість лінії регресії дуже добра. Коефіцієнт кореляції
може набути найбільшого значення 1, то можна сказати, що якість лінії регресії дуже добра. Коефіцієнт кореляції 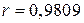 показує, що дві змінні, споживацькі витрати і дохід, високопозитивно корельовані.
показує, що дві змінні, споживацькі витрати і дохід, високопозитивно корельовані.
Дата добавления: 2016-07-27; просмотров: 2390;











