Інтервальні оцінки: основні ідеї
Для демонстрації підходу розглянемо гіпотетичний приклад «сімейний дохід - витрати на споживацькі товари», наведений раніше. Рівняння (2.6.2) показує, що гранична схильність до споживання (MPC, marginal propensity toconsume) 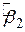 дорівнює 0,5091, має точкове значення невідомого МРС
дорівнює 0,5091, має точкове значення невідомого МРС  . Наскільки ця оцінка достовірна? Як зазначено в розд. 2, унаслідок вибіркових флуктуацій точкове значення швидше за все відрізняється від істинного
. Наскільки ця оцінка достовірна? Як зазначено в розд. 2, унаслідок вибіркових флуктуацій точкове значення швидше за все відрізняється від істинного  , хоча при повторних вибірках її математичне сподівання дорівнює
, хоча при повторних вибірках її математичне сподівання дорівнює  , оскільки
, оскільки 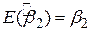 . У статистиці достовірність точкового значення вимірюється її стандартною помилкою. Отже, замість того, щоб покладатися лише на точкове значення, ми можемо побудувати інтервал навкруги точки оцінювання, скажімо у дві або три стандартні помилки вліво і вправо від точки, так що цей інтервал містить, скажімо, з імовірністю 95% істинне значення параметра. У цьому полягає ідея інтервальної оцінки.
. У статистиці достовірність точкового значення вимірюється її стандартною помилкою. Отже, замість того, щоб покладатися лише на точкове значення, ми можемо побудувати інтервал навкруги точки оцінювання, скажімо у дві або три стандартні помилки вліво і вправо від точки, так що цей інтервал містить, скажімо, з імовірністю 95% істинне значення параметра. У цьому полягає ідея інтервальної оцінки.
Припустимо, що ми хочемо знайти наскільки “близько” розташована 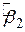 до
до  . Для цього спробуємо знайти такі два позитивних числа
. Для цього спробуємо знайти такі два позитивних числа 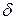 і
і 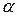 , останнє знаходиться між 0 і 1, що випадковий інтервал
, останнє знаходиться між 0 і 1, що випадковий інтервал 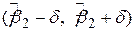 містить істинне значення
містить істинне значення  з імовірністю
з імовірністю 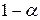 . У математичних позначеннях це записується як
. У математичних позначеннях це записується як
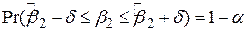 . .
| (3.1.1) |
Такий інтервал, якщо він, звичайно, існує, має назву довірчого інтервалу; 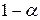 називається довірчим коефіцієнтом, а
називається довірчим коефіцієнтом, а 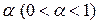 відомий як рівень (ступінь) значимості (level significance). Кінці довірчого інтервалу називаються межами довіри (confident limits): (
відомий як рівень (ступінь) значимості (level significance). Кінці довірчого інтервалу називаються межами довіри (confident limits): ( 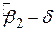 ) – нижня межа довіри і (
) – нижня межа довіри і ( 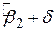 ) – верхня межа довіри. На практиці
) – верхня межа довіри. На практиці 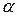 і (
і ( 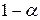 ) часто виражаються у відсотках.
) часто виражаються у відсотках.
Рівняння (3.1.1) показує, що на противагу точковій оцінці інтервальна оцінка є інтервалом, побудованим таким чином, що він містить з певною імовірністю ( 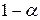 ) істинне значення параметра. Наприклад, якщо
) істинне значення параметра. Наприклад, якщо 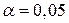 або 5%, (3.1.1) свідчить таке: імовірність того, що випадковий інтервал у (3.1.1) містить істинне значення
або 5%, (3.1.1) свідчить таке: імовірність того, що випадковий інтервал у (3.1.1) містить істинне значення  , дорівнює 0,95 або 95%. Інтервальна оцінка дає, таким чином, інтервал, у якому може лежати істинне значення
, дорівнює 0,95 або 95%. Інтервальна оцінка дає, таким чином, інтервал, у якому може лежати істинне значення  .
.
Важливо знати такі аспекти інтервальної оцінки:
1. Рівняння (3.1.1) не свідчить про те, що імовірність того, що  лежить між фіксованими межами, дорівнює
лежить між фіксованими межами, дорівнює 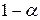 , оскільки
, оскільки  , хоч воно і невідоме, не фіксоване число, не можна сказати, лежить воно усередині інтервалу чи ні. Формула (3.1.1) стверджує, що застосовуючи описаний вище метод, імовірність побудови інтервалу, який містить
, хоч воно і невідоме, не фіксоване число, не можна сказати, лежить воно усередині інтервалу чи ні. Формула (3.1.1) стверджує, що застосовуючи описаний вище метод, імовірність побудови інтервалу, який містить  , дорівнює
, дорівнює 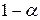 .
.
2. Інтервал (3.1.1) - випадковий, тобто він змінюватиметься (варіюватиметься) від однієї вибірки до іншої, оскільки в його основі лежить 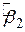 , що є випадковим.
, що є випадковим.
3. Оскільки довірчий інтервал є випадковим, твердження імовірності, що стосується нього, слід розуміти в значенні тривалого повторення вибірок. Більш точно (3.1.1) стверджує: якщо в повторних вибірках довірчі інтервали, подібні побудованому, отримані в результаті великої кількості вибірок на базі ймовірності 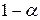 , то в середньому такі інтервали будуть містити в
, то в середньому такі інтервали будуть містити в 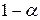 випадках істинне значення параметра
випадках істинне значення параметра  .
.
4. Як зазначено в пункті 2, інтервал (3.1.1.) випадковий, поки 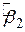 невідомий. Але якщо ми взяли конкретну вибірку і отримали конкретне числове значення
невідомий. Але якщо ми взяли конкретну вибірку і отримали конкретне числове значення 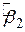 , то інтервал (3.1.1) більше не випадковий, а фіксований. У цьому випадку ми не можемо стверджувати (3.1.1) про імовірність, тобто ми не можемо сказати, що з імовірністю
, то інтервал (3.1.1) більше не випадковий, а фіксований. У цьому випадку ми не можемо стверджувати (3.1.1) про імовірність, тобто ми не можемо сказати, що з імовірністю 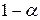 фіксований інтервал містить істинне значення
фіксований інтервал містить істинне значення  . При цьому
. При цьому  або лежить усередині інтервалу, або поза ним. Отже, імовірність цієї події дорівнює 1 або 0. Так, для нашого гіпотетичного прикладу “споживання-дохід” якщо 95%-й довірчий інтервал був отриманий як (
або лежить усередині інтервалу, або поза ним. Отже, імовірність цієї події дорівнює 1 або 0. Так, для нашого гіпотетичного прикладу “споживання-дохід” якщо 95%-й довірчий інтервал був отриманий як ( 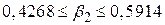 ), ми не можемо сказати, що з імовірністю 95% цей інтервал містить істинне
), ми не можемо сказати, що з імовірністю 95% цей інтервал містить істинне  . Імовірність становить 1 або 0.
. Імовірність становить 1 або 0.
Як будується довірчий інтервал? З огляду на вищезазначене можна сподіватися, що якщо розподіл імовірності оцінювачів відомий, то можна побудувати довірчий інтервал (3.1.1). Ми знаємо, що при припущенні про нормальність закону розподілу 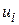 отримані за МНК оцінки
отримані за МНК оцінки 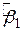 і
і 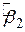 також нормально розподілені, а оцінка за МНК
також нормально розподілені, а оцінка за МНК 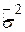 пов’язана з розподілом
пов’язана з розподілом  . Покажемо, що процедура побудови довірчого інтервалу - нескладна задача.
. Покажемо, що процедура побудови довірчого інтервалу - нескладна задача.
3.2 Довірчі інтервали для регресійних коефіцієнтів 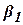 і
і 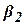
Як було відзначено раніше, при припущенні про нормальний закон розподілу залишків 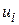 отримані за МНК оцінки
отримані за МНК оцінки 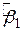 і
і 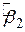 самі розподілені за нормальним законом з відомими математичними сподіваннями і дисперсіями:
самі розподілені за нормальним законом з відомими математичними сподіваннями і дисперсіями:
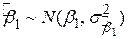 , , 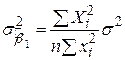 , ,
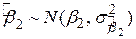 , , 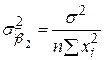 . .
|
Дата добавления: 2016-07-27; просмотров: 2163;











