Властивості логічних функцій
Властивості логічних функцій розглянемо на прикладі двозначної логічної функції 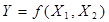 яка на практиці зустрічається найчастіше. Для цього складемо табл. 1.5 всіх можливих наборів аргументів у вигляді двійкових чисел: 00, 01, 10, 11; всі 16 значень функції розміщено у порядку зростання двійкових чисел (від 0000 до 1111).
яка на практиці зустрічається найчастіше. Для цього складемо табл. 1.5 всіх можливих наборів аргументів у вигляді двійкових чисел: 00, 01, 10, 11; всі 16 значень функції розміщено у порядку зростання двійкових чисел (від 0000 до 1111).
Таблиця 1.5 Двозначні логічні функції
| Фун-кція | Набір аргументів | Назва логічної функції | Визначення логічної Функції | |||
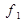
| Константа нуль | |||||
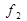
| Кон’юнкція | 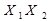
| ||||
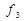
| Заборона 
| 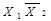
| ||||
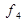
| Повторення 
| 
| ||||
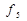
| Заборона 
| 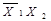
| ||||
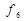
| Повторення 
| 
| ||||
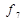
| Виняткове АБО |  Å Å 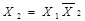 v v 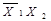
| ||||
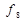
| Диз’юнкція |  v v 
| ||||
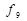
| Функція Пірсона | 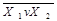
| ||||
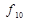
| Рівнозначність |  ~ ~ 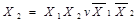
| ||||
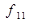
| Інверсія 
| 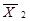
| ||||
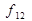
| Імплікація від  до до 
| 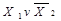
| ||||
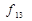
| Інверсія 
| 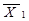
| ||||
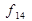
| Імплікація від  до до 
| 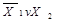
| ||||
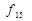
| Функція Шефера | 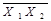
| ||||
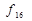
| Константа одиниця |
Всі наведені 16 логічних Функцій на практиці не застосовуються, бо, як видно з табл. 1.5, яка, до речі, має симетрію, функції 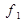 і
і 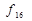 тривіальні,
тривіальні, 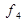 ,
, 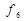 ,
, 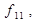
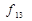 - не залежать від одного з аргументів. Хоча решта десять функцій залежать від двох аргументів, однак і серед них е такі, які можна одержати через інші.
- не залежать від одного з аргументів. Хоча решта десять функцій залежать від двох аргументів, однак і серед них е такі, які можна одержати через інші.
Аналогічно арифметичним операціям у бульовій алгебрі також існує поняття "першості виконання" операції, що визначає, яка з логічних операцій має виконуватися раніше. Отже, для логічних операцій першість визначається у такій послідовності: 1 - заперечення, 2 –кон’юнкція, 3 – диз’юнкція, 4 - імплікація, 5 - рівнозначність. При наявності у виразі логічної функції круглих дужок ступінь першості збільшується на одиницю.
Зауважимо, що деякі з наведених у табл. 1.5 функцій одержують методом перенумерації (перейменування або декомпозиції) аргументів логічних функцій. Наприклад, функція 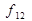 отримується з функції
отримується з функції 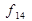 , якщо
, якщо  перенумерувати на
перенумерувати на  і навпаки, беручи набір аргументів справа наліво або зліва направо. Функцію
і навпаки, беручи набір аргументів справа наліво або зліва направо. Функцію 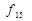 можна отримати з функції
можна отримати з функції 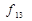 підстановкою замість
підстановкою замість  іншою функції
іншою функції 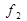 (тобто проінвертувавши набір аргументів). Така операція називається суперпозицією. Отже, застосовуючи метод суперпозицій, можна одержати більш складні логічні функції. При цьому виникає питання, чи можливий набір більш простих функцій, за допомогою яких можна було б отримати як завгодно складну логічну функцію. З практичної точки зору це дуже важливе питання, бо воно стосується технології виготовлення мікросхем і т. ін. З теоретичної точки зору воно пов’язане з основним поняттям бульової алгебри - функціональною повнотою системи логічних функцій.
(тобто проінвертувавши набір аргументів). Така операція називається суперпозицією. Отже, застосовуючи метод суперпозицій, можна одержати більш складні логічні функції. При цьому виникає питання, чи можливий набір більш простих функцій, за допомогою яких можна було б отримати як завгодно складну логічну функцію. З практичної точки зору це дуже важливе питання, бо воно стосується технології виготовлення мікросхем і т. ін. З теоретичної точки зору воно пов’язане з основним поняттям бульової алгебри - функціональною повнотою системи логічних функцій.
Набір (система) бульових функцій вважається функціонально повним. якщо на його основі або на базисі можна отримати довільну бульову Функцію, застосовуючи лише метод суперпозиції.
Функціонально повних наборів-базисів можна отримати досить багато. Найбільш поширені серед них наведені в табл. 1.6.
Найпростішим /елементарним/ базисом, що є основою бульової алгебри, е набір трьох основних логічних функцій (або операцій): 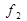 і
і 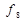 ,
, 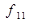 або
або 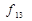 , на яких зупинимося більш детальніше (табл. 1.5, 1.6):
, на яких зупинимося більш детальніше (табл. 1.5, 1.6):
інверсія - логічне заперечення або функція НЕ; ця функція згадувалася раніше як однозначна, а тепер розглядається як двозначна ( 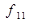 і
і 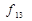 ), хоча залежить тільки від одної з двох змінних,
), хоча залежить тільки від одної з двох змінних,
диз’юнкція - логічне додавання або функція АБО, яка істинна тоді, коли істинні або  , або
, або  , або обидві змінні;
, або обидві змінні;
кон’юнкція - логічне множення або функція І, яка істинна тільки тоді, коли і  і
і  істинні.
істинні.
До більш спрощених базисів, з допомогою яких можна побудувати будь-яку складну цифрову систему обробки інформації, належить, наприклад, набір з двох елементарних логічних функцій 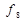 і
і 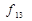 або
або 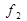 і
і 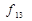 і навіть набір лише з одної логічної функції
і навіть набір лише з одної логічної функції 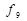 або
або 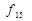 . Решту логічних функцій, які відсутні у цих базисах, можна одержати на основі правил (законів) алгебри логіки.
. Решту логічних функцій, які відсутні у цих базисах, можна одержати на основі правил (законів) алгебри логіки.
Елементи, що реалізують бульові (логічні) операції, називаються логічними елементами (ЛЕ). Якщо логічні операції і прийнято зображати у вигляді формул, то ЛЕ - графічно у вигляді схем. Умовне графічне позначення ЛЕ прийнято зображати прямокутником, у якого лінії зліва - входи аргументів 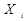 , справа –функція
, справа –функція 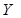 . Тип логічної операції задається спеціальною позначкою: інверсія – кружком на вході або виході (ЛЕ - інвертор), диз’юнкція - 1, кон’юнкція - & (табл. 1.6).
. Тип логічної операції задається спеціальною позначкою: інверсія – кружком на вході або виході (ЛЕ - інвертор), диз’юнкція - 1, кон’юнкція - & (табл. 1.6).
Таблиця 1.6 Основні логічні функції.
| Вхідні змінні | Диз’юн-кція
АБО:
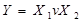 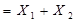
| Кон’нкція
І:
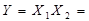 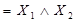
| Штрих
Шефера
І-НЕ:
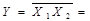 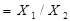
| Стрілка Пірса
АБО-НЕ
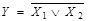 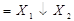
| Вийняткове АБО:
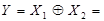 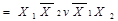
| Вийняткове
АБО-НЕ
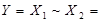 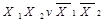
| |

| 
| ||||||
| Назва і умовне /схемне/ позна- чення | Диз’юн-
ктор
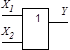
| Кон’юн-ктор 
| Елемент
Шефера 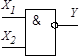
| Елемент
Пірса 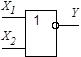
| Суматор
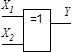
| Суматор інвертор 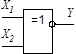
|
Логічні функції багатьох змінних одержують аналогічно розглянутому випадку 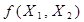 застосуванням методу суперпозиції та аксіом і законів алгебри логіки. Слід зауважити, що базисні функції обов'язково містять у собі операцію інверсії. Побудовані на їх основі логічні елементи (наприклад, на елементах Шефера або Пірса) дозволяють будувати функціональні вузли цифрових систем будь-якої складності.
застосуванням методу суперпозиції та аксіом і законів алгебри логіки. Слід зауважити, що базисні функції обов'язково містять у собі операцію інверсії. Побудовані на їх основі логічні елементи (наприклад, на елементах Шефера або Пірса) дозволяють будувати функціональні вузли цифрових систем будь-якої складності.
Особливий інтерес для практики має функція 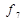 сума за модулем 2, яку ще називають “виняткове АБО". Логічний елемент-суматор за модулем 2, що реалізує цю функцію, широко застосовують у різних цифрових функціональних пристроях комбінаційного типу.
сума за модулем 2, яку ще називають “виняткове АБО". Логічний елемент-суматор за модулем 2, що реалізує цю функцію, широко застосовують у різних цифрових функціональних пристроях комбінаційного типу.
Особливість функції “виключне АБО” в тому, що вона збігається з функцією АБО в усіх випадках, за винятком, одного, коли всі змінні набувають значення одиниці, а саме при 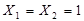 . 3 цієї причини, очевидно, ця функція й називається "виняткове АВО” Символ Å псевдоплюс означає, що змінні (аргументи)
. 3 цієї причини, очевидно, ця функція й називається "виняткове АВО” Символ Å псевдоплюс означає, що змінні (аргументи)  і
і  пов’язані логічною функцією “вийняткове АБО” яка істинна тоді, коли одна із змінних (
пов’язані логічною функцією “вийняткове АБО” яка істинна тоді, коли одна із змінних (  або
або  ) є істинною:
) є істинною:
 Å
Å 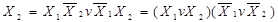
Виняткове АБО (цю функцію ще називають нерівнозначністю або нееквівалентністю) має властивості:
комутативності  Å
Å  =
=  Å
Å  ;
;
асоціативності  Å
Å 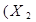 Å
Å 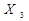 )=(
)=(  Å
Å  )Å
)Å 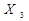 ;
;
дистрибутивності відноснокон’юнкції 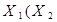 Å
Å 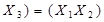 Å
Å 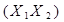 .
.
Справедливі також аксіоми 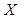 Å 0
Å 0 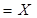 ;
; 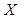 Å
Å 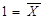 ;
; 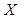 Å
Å 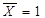 ;
; 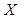 Å
Å 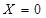 .
.
На основі властивостей і аксіом функції ''вийняткове АВО” можна одержати функцію елементарного базису:
НЕ - 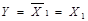 Å 1; І -
Å 1; І - 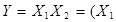 Å
Å 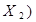 Å
Å 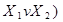 ;
;
АБО - 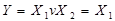 Å
Å  Å
Å 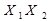
Для функції “вийняткове АБО-НЕ” (рівнозначність або еквівалентність) справедлива така рівність:
 ~
~ 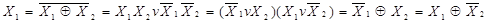
Дата добавления: 2016-07-22; просмотров: 4045;











