Властивості матриці інцидентності

- кожний стовпець матриці інцидентності обов’язково містить два одиничних елемента (для орграфа вони мають різні знаки);

- кількість одиниць в рядку дорівнює степені відповідної вершини (для орграфа - кількість одиниць зі знаком «+» визначає позитивну напівстепінь, кількість одиниць зі знаком «-» – негативну напівстепінь;

- нульовий рядок відповідає ізольованій вершині;

- нульовий стовпчик відповідає петлі.

Суміжність. Задання графа за допомогою матриці суміжності.

Матриця суміжності графа — це квадратна матриця A= 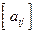, стовпцям і рядкам якої відповідають вершини графа. Для неорієнтованого графа a_ij дорівнює кількості ребер, інцидентних i-та j -й вершинам, для орієнтованого графа цей елемент матриці суміжності відповідає кількості ребер з початком в і-й вершині й кінцем j -й. Таким чином, матриця суміжності неорієнтова­ного графа є симетричною (a_ij = a_ji), а орієнтованого — необов'язково. Якщо вона все ж симетрична, то для кожного ребра орієнтованого графа існує ребро, яке з'єднує ті самі вершини, але йде у зворотному напрямку. Очевидно, орієнтований граф із симетричною матрицею суміжності канонічно відповідає неорієнтованому графу, що має ту саму матрицю суміжності.

Матриці суміжності розглянутих вище графів (див. рис. 2 і 3) наведено в табл. 2. Матриця суміжності повністю визначає відповідний неорієнтова-ний або орієнтований граф. Число його вершин дорівнює вимірності матриці п, і- та j-й вершинам графа інцидентними є a_ij ребер. Для неорієнтованого графа a_ij = a_ji., і всі його ребра визначаються верхнім правим трикутником матриці, розташованим над діагоналлю, включаючи останню.

Таблиця 2.

	v1 v2 v3 v4 v5
v1 v2 v3 v4 v5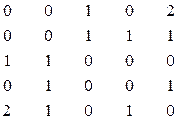

Властивості матриці суміжності

- матриця суміжності не орієнтованого графа завжди симетрична до головної діагоналі.;

- елементи на головній діагоналі завжди дорівнює 0, тільки коли є петля тоді елементи на головній діагоналі дорівнює 1;

- матриця суміжності орієнтованого графа в загальному випадку не симетрична відносно головної діагоналі;

- в стовпчиках або рядках, відповідних ізольованим вершинам, усі елементи дорівнюють 0.

степені вершин графа

Якщо задано матриці суміжності А або інцидентності S графа, то можна визначити локальні степені всіх його вершин. Справді, в j-му стовпці матриці інцидентності, що відповідає вершині v_j одиниці зна­ходяться на перетині з рядками, яким відповідають інцидентні цій вершині ребра, а інші елементи стовпця дорівнюють 0. Отже,

r (v_j) = .

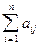При підрахунку степенів вершин за цими формулами кожна петля вно­сить у степінь інцидентної їй вершини 1. Проте при зображенні петлі на рисунку до цієї вершини примикають два кінці петлі, тобто петля вно­сить у цей степінь 2. Щоб таким чином ураховувати внесок петель у степінь, треба трохи ускладнити формули для його обчислення. Через ко­ефіцієнти матриці інцидентності степінь можна розрахувати, наприклад, за формулою

Означення . Звичайний граф називається повним, якщо кожна пара