Точність або стандартна похибка оцінювачів за МНК

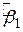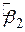З рівнянь (2.1.15), (2.1.16) зрозуміло, що оцінювачі і за МНК - функція від даних вибірки. Але оскільки дані можуть змінюватися від вибірки до вибірки, то змінюватимуться й значення оцінювачів. Отже, необхідна міра «достовірності» або точності обчислення оцінювачів 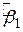і 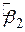. У статистиці точність оцінювача вимірюється його стандартною похибкою. Як зазначено раніше при прийнятих гіпотезах оцінювачі за МНК мають такі значення дисперсій і стандартної похибки:

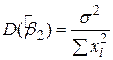;	(2.3.1)
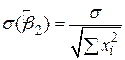,	(2.3.2)
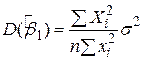;	(2.3.3)
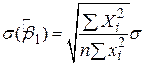;	(2.3.4)

де 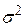- дисперсія 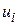. Усі величини, що входять у (2.3.1)–(2.3.4), за виключенням 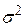, можна підрахувати за даними вибірки. Для самої ж величини 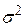справедлива формула

,

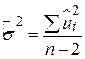(2.3.5)

де 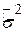- оцінка за МНК істинного значення 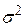. Величина (N–2) має назву кількості степенів вільності (df, number degrees freedom). 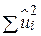- сума квадратів залишків RSS (residual sum squares).

Оскільки 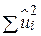відома, то 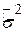може бути легко обчислений. Сама величина 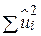може бути обчислена за формулою

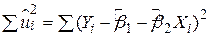
або

.

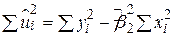(2.3.6)

Зауважимо, що формула (2.3.6) простіша в застосуванні порівняно з (2.1.2), тому що не вимагає обчислення 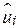для кожного i, хоча саме таке обчислення виявляється корисним.

Оскільки

,

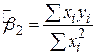з (2.3.6) можна отримати ще один вираз для підрахунку :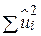

.

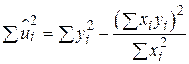(2.3.7)

Позитивний квадратний корінь з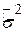

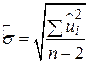
(2.3.8)

називається стандартною похибкою оцінювача. Вона є стандартним відхиленням величин Y від оціненої лінії регресії і часто застосовується як сумарна міра “якості підгонки” оціненої лінії регресії.

Відзначимо такі властивості дисперсії (а отже, і стандартної похибки) коефіцієнтів 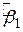і .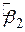

1. Дисперсія коефіцієнта 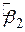прямо пропорційна 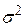, але обернено пропорційна 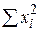. Тобто для даного 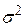, чим більша область зміни величин Х, тим менша дисперсія 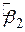і, отже, вища точність, з якою може бути оцінений 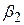. Коротше кажучи, при значній зміні величин Х коефіцієнт 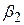може бути виміряний більш точно, ніж при незначній зміні величин Х. Крімтого, для даної величини 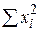чим більше 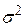, тим більша дисперсія 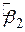. Зауважимо, що зі збільшенням обсягу вибірки N, кількість членів у 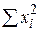зростатиме. Тому зі зростанням N точність оцінки коефіцієнта 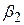збільшуватиметься.

2. Дисперсія коефіцієнта 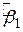прямо пропорційна 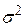і 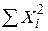, але обернено пропорційна 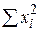і розміру вибірки N.

3. Оскільки 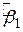і 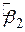є оцінками, вони будуть не тільки змінюватися від вибірки до вибірки, але й будуть взаємно залежними в межах однієї вибірки. Ця залежність вимірюється коваріацією між ними. Пізніше буде показано, що

.

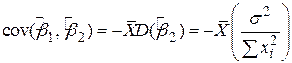(2.3.9)

Оскільки 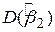завжди позитивна, коваріація між 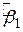і 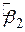залежить від знака 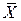. Якщо 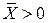, тоді, як бачимо з формули (2.3.9), коваріація буде негативна. Так, якщо кутовий коефіцієнт 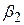оцінений із завищенням (тобто лінія регресії підіймається із завищеною крутістю) коефіцієнт перетину 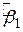матиме занижене значення (перетин матиме менше значення).