Диференціальні рівняння першого порядку.
План
1. Основні поняття.
2. Задача Коші.
Основні поняття
Означення. Диференціальним рівнянням називається рівняння, яке містить похідну шуканої функції. Найбільший порядок похідних називається порядком диференціального рівняння.
У загальному випадку диференціальне рівняння n-го порядку має вигляд
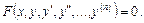
Далі замість слів «диференціальні рівняння» використовуватимемо позначення ДР.
| Приклад. | 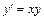
| — ДР першого порядку; |
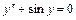
| — ДР другого порядку; | |
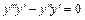
| — ДР третього порядку. |
Диференціальне рівняння може визначити функцію багатьох змінних.
Приклад.Рівняння з частинними похідними
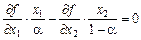
Має розв’язок
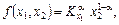
який називається функцією Кобба—Дугласа.
У запропонованому розділі розглянути лише диференціальні і різницеві рівняння, в яких шукана функція залежить лише від одного аргументу. Такі рівняння називаються звичайними.
У даній темі вивчаємо ДР першого порядку, які в загальному вигляді можна записати рівнянням
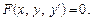 (9.1)
(9.1)
Це — ДР рівняння, що не розв’язане відносно похідної. Якщо рівняння (8.1) можна розв’язати відносно похідної, то рівняння (8.1) подаємо у вигляді
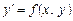 . (9.2)
. (9.2)
Це ДР рівняння, що розв’язане відносно похідної, і його можна записати у вигляді 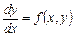 або
або 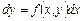 .
.
Якщо 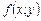 є дробом,
є дробом, 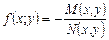 , тоді ДР першого порядку можна записати в симетричній формі
, тоді ДР першого порядку можна записати в симетричній формі
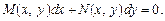 (9.3)
(9.3)
Означення. Розв’язком ДР 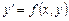 називається функція
називається функція 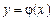 , яка при підстановці у ДР перетворює його на тотожність. Графік функції
, яка при підстановці у ДР перетворює його на тотожність. Графік функції 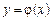 називається інтегральною кривою.
називається інтегральною кривою.
Приклад. Задача інтегрування функцій може бути розглянута як задача інтегрування ДР
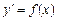
і має розв’язок
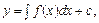
який знаходиться інтегруванням, тобто квадратурою.
Інтегральні криві утворюються зсувом однієї з них вздовж осі у.
Приклад. ДР 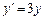 має розв’язок
має розв’язок 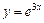 .
.
l Справді, 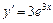 . Підставивши
. Підставивши 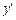 в рівняння, дістанемо тотожність
в рівняння, дістанемо тотожність 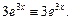
Звичайно, ДР має нескінченну множину розв’язків. Так, попереднє рівняння 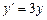 має розв’язок
має розв’язок 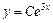 , де С — довільний параметр.
, де С — довільний параметр.
Задача Коші
Розглянемо ДР 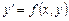 .
.
Означення.Задача пошуку розв’язку 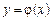 , що задовольняє умови
, що задовольняє умови
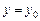 при
при 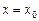 (9.4)
(9.4)
називається задачею Коші. Умови (9.4) називаються початковими умовами, числа 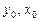 називаються початковими значеннями.
називаються початковими значеннями.
Означення. Точки, в яких порушується єдиність розв’язків ДР, називаються особливими. Розв’язок ДР називається особливим, коли всі точки на розв’язку особливі.
Якщо в диференціальному рівнянні першого порядку
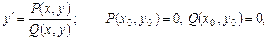
то точка 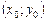 є особливою точкою ДР.
є особливою точкою ДР.
Наведемо приклади поводження інтегральних кривих в околі особливої точки (рис. 9.1).
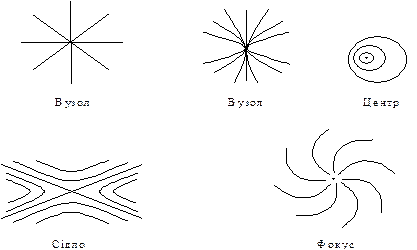 Рис. 9.1
Рис. 9.1
Приклад.Розглянемо ДР 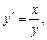 яка має особливу (0; 0). Розв’яжемо ДР
яка має особливу (0; 0). Розв’яжемо ДР 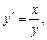
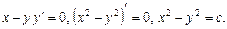
Інтегральними кривими є гіперболи. Особлива точка (0; 0) є сідлом.
Розглянемо ДР 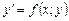 .
.
Означення. Функція 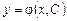 , що містить довільну сталу С, називається загальним розв’язком ДР, якщо функція
, що містить довільну сталу С, називається загальним розв’язком ДР, якщо функція 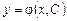 є розв’язком ДР при довільному значенні сталої С, тобто
є розв’язком ДР при довільному значенні сталої С, тобто 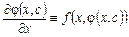 і за рахунок вибору довільної сталої С можна розв’язати задачу Коші з довільними початковими умовами, тобто рівняння
і за рахунок вибору довільної сталої С можна розв’язати задачу Коші з довільними початковими умовами, тобто рівняння 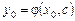 розв’язується відносно С. Розв’язок
розв’язується відносно С. Розв’язок 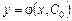 при фіксованому значенні сталої С називається частинним розв’язком.
при фіксованому значенні сталої С називається частинним розв’язком.
Приклад. ДР 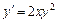 має загальний розв’язок
має загальний розв’язок 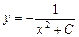
l Справді, маємо тотожність:
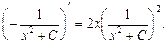
При довільних початкових значеннях 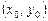 ,
, 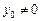 знаходимо значення довільної сталої С
знаходимо значення довільної сталої С
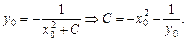
Якщо довільна стала виражена через початкові дані, то загальний розв’язок називається розв’язком у формі Коші.
Приклад. ДР 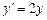 має розв’язок
має розв’язок 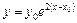 у формі Коші.
у формі Коші.
Означення. Задача знаходження розв’язків ДР називається інтегруванням ДР. Самий розв’язок називається також інтегралом ДР. Назва пояснюється розв’язуванням найпростішого ДР 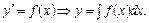
Загальний розв’язок може бути знайдений у неявній формі: 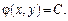 Тоді ця рівність називається інтегралом ДР. Функція
Тоді ця рівність називається інтегралом ДР. Функція 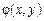 також називається інтегралом ДР. Якщо загальний розв’язок ДР подається неявним рівнянням
також називається інтегралом ДР. Якщо загальний розв’язок ДР подається неявним рівнянням 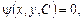 то рівняння називається загальним інтегралом ДР.
то рівняння називається загальним інтегралом ДР.
Розв’яжемо диференціальне рівняння
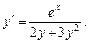
Рівняння можна записати у вигляді
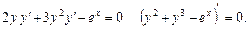
Звідси знаходимо інтеграл ДР 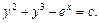
Розглянемо детальніше питання про особливі розв’язки. Точки, в яких існує не єдиний розв’язок ДР 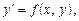 можуть бути точками розриву функцій
можуть бути точками розриву функцій 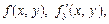 а також точками, в яких загальний інтеграл ДР
а також точками, в яких загальний інтеграл ДР 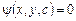 не розв’язуваний відносно с, тобто
не розв’язуваний відносно с, тобто 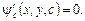 Криві, в точках яких не виконані умови єдиності рішень, називають дискримінантними кривими.
Криві, в точках яких не виконані умови єдиності рішень, називають дискримінантними кривими.
Приклад. Розв’яжемо ДР 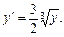
l Його можна записати у вигляді
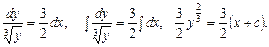
ДР має загальний інтеграл 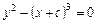 і загальний розв’язок
і загальний розв’язок 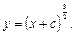
Шукаємо особливі розв’язки з умови 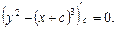
Знаходимо 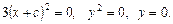
Дискримінантна крива y = 0 є розв’язком ДР, але не є частинним розв’язком. Цей особливий розв’язок можна було знайти з умови, що частина похідна
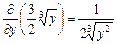 має розрив при y = 0. Інтегральні криві наведено на рис. 9.2.
має розрив при y = 0. Інтегральні криві наведено на рис. 9.2.
 Рис. 9.2
Рис. 9.2
Не завжди дискримінантна крива визначає рішення ДР.
Приклад.ДР 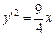 має загальний розв’язок
має загальний розв’язок 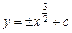 і загальний інтеграл
і загальний інтеграл 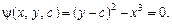
З умови 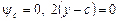 знаходимо дискримінантну криву
знаходимо дискримінантну криву
х = 0, яка не визначає ніякого рішення ДР. Інтегральні криві ДР зображено на рис. 9.3.
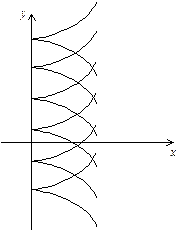 Рис. 9.3
Рис. 9.3
Дата добавления: 2016-05-26; просмотров: 2264;











