Ознака порівняння в граничній формі.

Означення. Якщо для рядів 10.6), (10.7) виконується умова 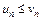, то ряд (10.7) називається мажорантним відносно ряду (10.6), а ряд (10.6) — мінорантним відносно ряду (10.7).

Приклад. Дослідити на збіжність ряд .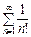

l Загальний член ряду 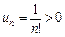. Зауважимо, що

.

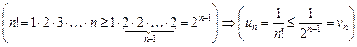Ряд порівняння 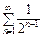збігається як ряд геометричної прогресії із 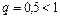. Значить, за ознакою порівняння (теорема 10.7) ряд 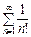— збігається.

Теорема 8 (ознака порівняння в граничній формі). Якщо для рядів з додатними членами (10.6), (10.7) існує границя 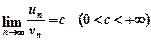, то ряди (10.6) і (10.7) збігаються або розбігаються разом.

Приклад. Дослідити на збіжність ряд .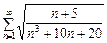

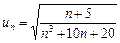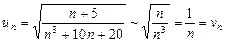l Загальний член ряду являє собою алгебраїчний вираз. Для того щоб цілеспрямовано вибрати ряд порівняння, побудуємо величину, еквівалентну при . Вибираємо ряд порівняння — гармонічний ряд, він є розбіжним. Обчислюємо

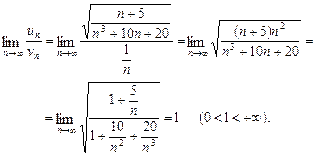
За ознакою порівняння (теорема 9.8) буде розбіжним і ряд

.

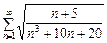Теорема 9 (ознака Даламбера). Якщо для ряду 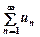з додатними членами 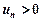існує границя 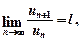тоді:

при 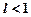ряд збігається;

при 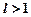ряд розбігається;

при 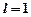питання про збіжність ряду ознака не вирішує.

Приклад. Дослідити на збіжність ряд .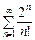

l Загальний член ряду 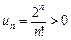. Побудуємо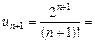 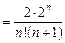і розглянемо 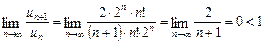. За ознакою Даламбера ряд 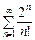збігається.

Теорема 10 (ознака Коші (радикальна)). Якщо для ряду 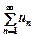з додатними членами 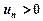існує границя 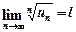, тоді:

при 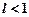ряд збігається;

при 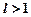ряд розбігається;

при 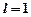питання про збіжність ряду ознака не вирішує.

Приклад. Дослідити на збіжність ряд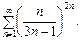

l Загальний член ряду .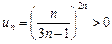

.

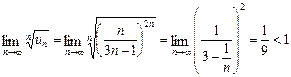За ознакою Коші (теорема 9.10) ряд збігається.

Теорема 11 (ознака Коші (інтегральна)). Якщо функція 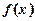неперервна, додатна і монотонно спадає при 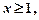то ряд 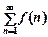і невластивий інтеграл 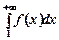збігаються або розбігаються разом.

Приклад. Дослідити на збіжність ряд Діріхле (узагальнений гармонічний ряд)

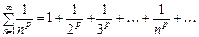(10.8)

l Загальний член ряду 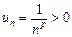. Побудуємо функцію :

.

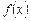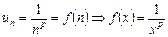Збіжність інтегралу Діріхле 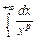встановлено в 7.3.1, таким чином, за теоремою 10.11

.

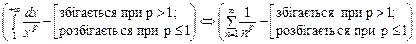У частинному випадку при р=1 маємо гармонічний ряд 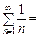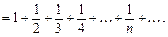який, як тепер встановлено, буде розбіжним.