Загальне рівняння динаміки механічної системи

При русі механічної системи, на яку накладені ідеальні в’язі, сума робот активних сил і сил інерції на будь-яких можливих переміщеннях матеріальних точок дорівнює нулю:

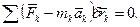(18.1)

Якщо

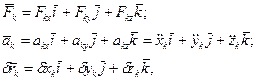
то загальне рівняння динаміки має вигляд

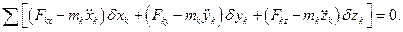(18.2)

Загальне рівняння динаміки є аналогом принципу можливих переміщень для випадку руху механічної системи.

Обчислення робот сил інерції на можливих переміщеннях точок твердого тіла проводиться за формулами:

а) при поступальному русі

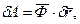(18.3)

де 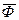- рівнодіюча сил інерції: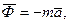 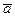- прискорення твердого тіла, 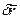- можливе переміщення твердого тіла;

б) при обертанні твердого тіла навколо нерухомої осі

(18.4)

де 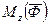- головний момент сил інерції відносно осі обертання z: 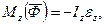І_z - момент інерції тіла відносно осі обертання z, ε_z - кутове прискорення тіла, δφ - можливе кутове переміщення твердого тіла;

в) при плоскому русі

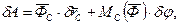(18.5)

де 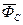- головний вектор сил інерції: 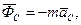m - маса тіла, 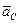- прискорення центра мас твердого тіла, 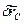- можливе переміщення центра мас твердого тіла, 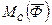- головний момент сил інерції відносно осі, яка проходить через центр мас С твердого тіла перпендикулярно до площини руху: 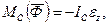І_С - момент інерції тіла відносно осі z, що проходить через центр мас, ε_z - кутове прискорення тіла, δφ - можливе кутове переміщення твердого тіла.

За допомогою загального рівняння динаміки можна розв’язати задачі динаміки механічної системи у випадках, коли в число заданих і шуканих величин входять: інерційні характеристики (маси і моменти інерції), лінійні прискорення точок системи і кутові прискорення тіл, активні сили і моменти, коефіцієнти тертя ковзання і кочення, коефіцієнти жорсткості пружин.

Якщо механічна система підпорядкована h голономним та ідеальним в’язям і має s ступенів вільності (має s узагальнених незалежних координат), то рівняння (18.1) можна записати так:

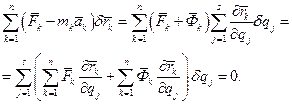(18.6)

Позначимо - узагальнена сила заданих сил, яка відповідає узагальненій координаті q_j ,

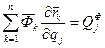- узагальнена сила сил інерції.

Тоді

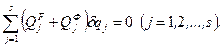(18.7)

Рівняння (18.7) - загальне рівняння динаміки механічної системи в узагальнених координатах. Розв’язувати задачі за допомогою загального рівняння динаміки потрібно в такій послідовності:

1) показати на рисунку активні сили і реакції, які відповідають неідеальним в’язям (наприклад, сили тертя);

2) визначити головні вектори і головні моменти сил інерції мас системи.

Подальші дії слід здійснювати в залежності від того, має система один ступінь вільності чи декілька.

Для систем з одним ступенем вільності:

3) дати можливе переміщення одній з точок системи і виразити через нього можливі переміщення точок прикладення всіх сил;

4) обчислити суму робот всіх сил на можливих переміщеннях системи, скласти загальне рівняння динаміки;

5) в загальному рівнянні динаміки скоротити на задане можливе переміщення, визначити шукану величину.

Для систем з декількома ступенями вільності:

3) вибрати незалежні можливі переміщення точок системи, їх число повинно бути рівним числу ступенів вільності;

4) надати можливого переміщення, що відповідає одному ступеню вільності системи, вважаючи, що всі інші можливі переміщення дорівнюють нулю. Виразити можливі переміщення через раніше вибране можливе переміщення;

5) обчислити суму робот всіх сил на відповідних можливих переміщеннях їх точок прикладання і прирівняти цю суму до нуля;

6) послідовно провести викладки пунктів 4) і 5) для кожного з можливих переміщень і скласти систему рівнянь рівноваги, число яких дорівнює числу ступенів вільності системи;

7) скоротити кожне з одержаних рівнянь на відповідне можливе переміщення, розв’язати систему рівнянь.

Примітка. При розв’язанні задач за допомогою загального рівняння динаміки зручно користуватись такими правилами:

1) зробити припущення про напрям прискорень точок системи;

2) направити на рисунку сили інерції протилежно вибраним напрямам відповідних прискорень;

3) знайти алгебраїчні величини головних векторів і головних моментів сил інерції;

4) обчислити суму робот всіх сил, прикладених до точок механічної системи, на кожному з можливих переміщень і скласти загальне рівняння ( систему рівнянь);

5) розв’язати одержане рівняння (систему рівнянь).