Стохастичні властивості PRF

З рис. 1.1 бачимо, що зі зростанням доходу сім’ї зростають у середньому і її витрати на споживацькі товари. Проте що можна сказати про витрати на споживання конкретної сім’ї з фіксованим рівнем доходу? З табл. 1.1 і рис. 1.1 бачимо, що зі зростанням доходу конкретної сім’ї рівень її витрат на споживання не обов'язково зростає. Наприклад, з табл. 1.1 бачимо, що в групі сімей із рівнем доходу 100 дол. є одна сім’я, чиї витрати на споживання складають 65 дол., що менше, ніж споживацькі витрати у двох сім’ях з групи з доходом 80 дол. Однак зауважимо, що середній рівень споживацьких витрат сімей із тижневим доходом 100 дол. вищий, ніж середній рівень споживацьких витрат у групі сімей із тижневим доходом 80 дол. (77 дол. проти 65 дол.).

Що тоді можна сказати про співвідношення між споживацькими витратами конкретної сім’ї і рівнем її доходу? З рис. 1.1 ми бачимо, що для даного рівня доходу споживацькі витрати сімей розташовуються біля середнього рівня споживацьких витрат групи сімей із тижневим доходом , тобто біля їх умовного сподівання. Отже, ми можемо виразити відхилення індивідуального 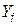від величини його сподівання таким чином:

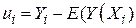або ,

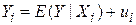(1.4.1)

де відхилення 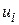- випадкова величина, що набуває як позитивних, так і негативних значень. Величину 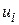називають стохастичним збуреннямабо складовою стохастичної помилки.

Яку інтерпретацію можна дати (1.4.1)? Можна сказати, що витрати індивідуальної сім’ї з фіксованим рівнем доходу можна подати у вигляді суми двох складових: 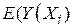, що позначає середній рівень витрат сімей з даним рівнем доходу. Цей доданок відомий як термін систематичноїабо детермінованоїскладової. Другий доданок - 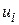, є випадкова величина, так звана несистематичнакомпонента. Згодом ми дослідимо природу 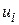, а зараз просто відзначимо, що вона містить усі опущені або знехтувані змінні, які можуть впливати на Y, але не включені в регресійну модель.

Якщо 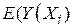передбачається лінійною функцією за , як це робилося в (1.2.2), то рівняння (1.4.1) можна переписати у вигляді

.

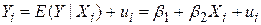(1.4.2)

Із рівняння (1.4.2) бачимо, що споживацькі витрати сім’ї лінійно пов’язані з її доходами плюс випадкова складова. Таким чином, індивідуальні витрати на споживацькі товари при X=80 дол. (див. табл. 1.1) можуть бути виражені

, , , , .

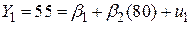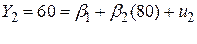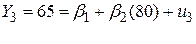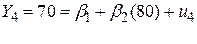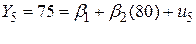(1.4.3)

Ураховуючи відомі властивості математичного сподівання:

1. Математичне сподівання сталої величини дорівнює самій сталій. Отже, якщо b є константа, то

E(b)=b.

2. Якщо а і b сталі, а X - випадкова величина, то

E(aX+b)=aE(X)+b.

Це правило може бути узагальнене. Якщо X₁, X₂ ...X_N - випадкові величини, а a₁, a_{2 .}..a_N і b -константи, то

E(a₁X₁+a₂X₂+...+a_NX_N+b)=a₁E(X₁)+a₂E(X₂)+...+a_NE(X_N)+b.

Обчислимо математичне сподівання від обох частин рівності (1.4.1):

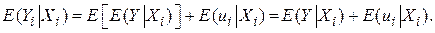
(1.4.4)

При цьому враховувалося, що математичне сподівання випадкової величини є величина стала. Оскільки в ліву і праву частини рівності (1.4.4) входять однакові величини E( 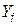½ ) і E(Y½ ), то легко одержуємо

.

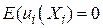(1.4.5)

Таким чином, припущення про те, що лінія регресії проходить через умовні середні Y,має на увазі, що математичне сподівання стохастичної складової 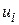дорівнює нулю.

Після цього стає зрозуміло, що рівності (1.2.2) і (1.4.2) еквівалентні, якщо для стохастичної складової виконується рівність (1.4.5). Проте стохастичне уточнення (1.4.2) має перевагу, оскільки показує, що окрім доходу сім’ї є й інші змінні, які впливають на споживацькі витрати конкретної сім’ї, і що витрати сім’ї не можуть бути повністю поясненими тільки змінною (змінними), включеними в модель.