Гіпотетичний приклад
РЕГРЕСІЙНИЙ АНАЛІЗ.
РЕГРЕСІЙНИЙ АНАЛІЗ ДЛЯ ДВОХ ЗМІННИХ: ОСНОВНІ ІДЕЇ
Як було зазначено у вступі, основним інструментом економетрики є регресійний аналіз. Зупинимося коротко на його суті.
Історичне походження терміна «регресія». Уперше термін “регресія” був введений Френсісом Галтоном[1] . Галтон установив таке: хоча й існує тенденція того, що у високих батьків народжуються високі діти, а в невисоких - невисокі, середній зріст дітей, народжених від батьків певного зросту, має тенденцію зміщуватися, “регресувати” в бік середнього зросту в популяції в цілому. Іншими словами, зріст дітей незвичайно високих або низьких батьків має тенденцію зміщуватися в бік середнього зросту популяції. Друг Галтона Карл Пірсон (Karl Pearson) за результатами зібраних ним даних про зріст у групах сімей підтвердив установлений Галтоном закон про універсальну регресію. Він установив, що середній зріст синів з групи високих батьків був менший, ніж середній зріст їх батьків, а середній зріст синів з групи низьких батьків був більший середнього зросту групи батьків, тобто високі й низькі сини «регресували» в бік середнього зросту чоловіків. Галтон охарактеризував це явище як регресію в бік звичайності.
Сучасна інтерпретація регресії. Сучасне значення, що вкладається в термін “регресія”, зовсім інше. У достатньо широкому значенні слова можна сказати, що регресійний аналіз пов’язаний із вивченням залежності однієї змінної, такої, що пояснюється, від однієї або декількох пояснювальних змінних, з метою обчислення і/чи прогнозування середньої величини першої при відомих (фіксованих) значеннях останніх.
Важливість такого підходу до поняття регресійного аналізу стане зрозумілішою в процесі заглиблення в економетрику.
Раніше ми обговорювали концепцію регресійного аналізу в широкому значенні. Зараз ми звернемо увагу на формальний бік предмета. Зокрема, ця частина присвячена введенню в теорію найпростішої регресійної моделі двох змінних. Її розгляд пов’язаний не стільки з важливістю практичного використання, скільки з поданням основних ідей регресійного аналізу в найпростішій формі, і може бути проілюстрований графічно двовимірними діаграмами. Більше того, як ми побачимо далі, більш загальний множинний регресійний аналіз багато в чому є логічним розвитком двовимірної моделі.
Гіпотетичний приклад
Як зазначалося раніше, регресійний аналіз займається головним чином обчисленням і/чи прогнозуванням середньої величини залежної змінної при фіксованих або передбачуваних значеннях пояснювальних змінних. Щоб зрозуміти, як це робиться, розглянемо гіпотетичний приклад. Уявимо собі гіпотетичну країну з населенням із 60 сімей. Припустимо, що нас цікавить вивчення зв’язку між тижневими споживацькими витратами Y і тижневим прибутком X після сплати податків. Нехай ми хочемо спрогнозувати середні тижневі споживацькі витрати, знаючи тижневий прибуток сім’ї.
Розділимо ці 60 сімей на 10 груп із приблизно однаковим прибутком і дослідимо споживацькі витрати в кожній групі. Гіпотетичні дані наведені в табл. 1.1.
Таблиця 1.1
Прибуток та витрати сімей за тиждень
| Тижневий прибуток сім’ї X, дол. | ||||||||||
| Витрати сім’ї за тиждень Y, дол. | ||||||||||
| - | - | - | ||||||||
| - | - | - | - | - | - | - | ||||
| Усього |
Табл. 1.1 можна інтерпретувати таким чином. У групі сімей із тижневим доходом у 80 дол. ( таких сімей п’ять) витрати на споживацькі товари змінюються від 55 до 75 дол. Аналогічно в групі сімей із тижневим доходом у X=240 дол. (шість сімей) витрати на споживацькі товари змінюються від 137 до 189 дол. Іншими словами, кожна колонка табл. 1.1 подає розподіл споживацьких витрат Y, відповідний фіксованому рівню доходу X. Тобто це дає умовний розподіл Y залежно від даної величини X.
Ураховуючи, що наведені в табл. 1.1 дані є повною групою результатів, ми можемо легко підрахувати умовну ймовірність Y при заданому значенні X, p(Y½X). Так, наприклад, для X=80 Y набуває одного з п’яти значень: 55 дол., 60 дол., 65 дол., 70 дол. і 75 дол. Отже, при даному X=80дол.ймовірність отримання будь-якого значення з указаних споживацьких витрат дорівнює 1/5. Умовимося позначати це таким чином: p(Y=55½X=80)=1/5. Аналогічно p(Y=150½X=260)=1/7 і т. д. Умовна ймовірність даних з табл. 1.1 наведена в табл. 1.2.
Таблиця 1.2
Умовна ймовірність p(Y½X) даних табл. 1.1
| X | ||||||||||
| p(Y½X), умовні ймовірності | 1/5 | 1/6 | 1/5 | 1/7 | 1/6 | 1/6 | 1/5 | 1/7 | 1/6 | 1/7 |
| 1/5 | 1/6 | 1/5 | 1/7 | 1/6 | 1/6 | 1/5 | 1/7 | 1/6 | 1/7 | |
| 1/5 | 1/6 | 1/5 | 1/7 | 1/6 | 1/6 | 1/5 | 1/7 | 1/6 | 1/7 | |
| 1/5 | 1/6 | 1/5 | 1/7 | 1/6 | 1/6 | 1/5 | 1/7 | 1/6 | 1/7 | |
| 1/5 | 1/6 | 1/5 | 1/7 | 1/6 | 1/6 | 1/5 | 1/7 | 1/6 | 1/7 | |
| - | 1/6 | - | 1/7 | 1/6 | 1/6 | - | 1/7 | 1/6 | 1/7 | |
| - | - | - | 1/7 | - | - | - | 1/7 | - | 1/7 | |
| Середнє значення |
Тепер для кожної умовної вірогідності розподілу Y ми можемо вирахувати середню величину витрат, відому як умовне середнє значення або умовне сподівання, що позначається E(Y½X=  ) (читається як “очікувана величина Y при X, що набуває конкретного значення
) (читається як “очікувана величина Y при X, що набуває конкретного значення  ”), яке скорочено ми записуватимемо як E(Y½
”), яке скорочено ми записуватимемо як E(Y½  ). Сподівання - середня величина витрат у групі. Для наших гіпотетичних даних ці умовні сподівання можна легко підрахувати шляхом множення відповідних значень Y з табл. 2.1 на їх умовну ймовірність і подальшим підсумовуванням добутків. Як приклад підрахуємо умовне середнє значення або сподівання Y при X = 80:
). Сподівання - середня величина витрат у групі. Для наших гіпотетичних даних ці умовні сподівання можна легко підрахувати шляхом множення відповідних значень Y з табл. 2.1 на їх умовну ймовірність і подальшим підсумовуванням добутків. Як приклад підрахуємо умовне середнє значення або сподівання Y при X = 80:
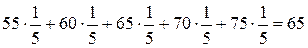 .
.
Підраховані таким чином умовні середні значення наведені в нижньому рядку табл. 1.2.
Перш ніж просуватися далі, подивимося на дані табл. 1.1, наведені на рис. 1.1. На рисунку точками зображений розподіл величин Y, відповідних різним значенням X. З рисунка бачимо, що хоча й існують відмінності за споживацькими витратами в окремих сім’ях, але зрозуміло, що середні споживацькі витрати сім’ї збільшуються зі зростанням доходу сім’ї.
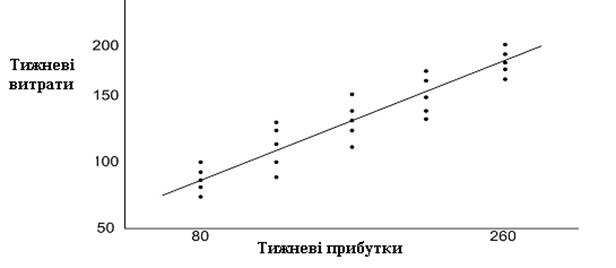
Рис. 1.1. Розподіл величин Y, відповідних різним значенням X
Це спостереження ще чіткіше простежується, якщо звернутися до зображення на координатній площині точок, що позначають умовні середні значення Y.
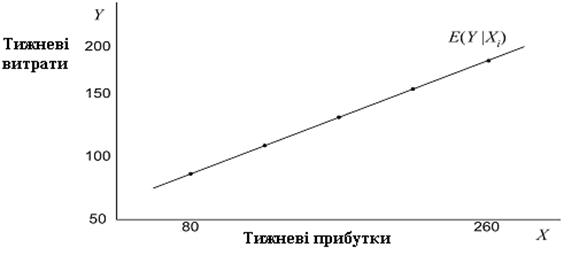
Рис. 1.2. Умовні середні значення Y
На рис.1.2 умовні середні значення лежать на прямій лінії з позитивним коефіцієнтом при X (При цьому слід пам’ятати, що ми розглядаємо гіпотетичні дані, а отже, умовні середні значення не обов’язково лежатимуть на прямій лінії, вони можуть лежати і на кривій). Ця лінія називається лінією регресії популяції або кривою популяції регресії. Більш просто, це регресія Y від X.
Геометричне значення таке: регресійна крива популяції - крива точок умовних середніх значень або сподівань залежної змінної від пояснювальної.
Регресійна крива популяції (рис. 1.2) показує, що кожній точці  відповідає розподіл значень і певне умовне середнє значення Y. Регресійна пряма або крива проходить через умовні середні значення.
відповідає розподіл значень і певне умовне середнє значення Y. Регресійна пряма або крива проходить через умовні середні значення.
Дата добавления: 2016-07-27; просмотров: 1830;











