Концепція регресійної функції популяції (PRF роpulation regression function)

З попередніх міркувань (особливо з рис. 1.1 і 1.2) зрозуміло, що кожне умовне середнє E(Y½ ) є функція від . Символічно це можна зобразити у вигляді

,

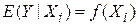(1.2.1)

де 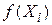позначає деяку функцію від пояснювальної змінної . У нашому гіпотетичному прикладі E(Y½ ) є лінійна функція від . Рівняння (1.2.1) відоме як двовимірна регресійна функція (роpulation regression function) популяції (PRF),яка стверджує, що середнє значення від розподілу Y для даного функціонально пов’язане з . Іншими словами, воно показує, як середнє Y змінюється зі зміною X.

Який вигляд має функція 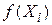? Це питання важливе, оскільки в реальній практичній ситуації ми не маємо у своєму розпорядженні повної сукупності даних для дослідження. Вигляд функції PRF є питання емпіричне, хоча в конкретному випадку теорія може дещо підказати. Наприклад, економіст може констатувати, що споживацькі витрати лінійно пов’язані з доходом сім’ї. Отже, як перше наближення або гіпотезу ми можемо припустити, що PRF E(Y½ ) є лінійна функція від , скажімо вигляду

,

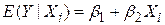(1.2.2)

де b₁ і b₂ - невідомі, але фіксовані параметри під назвою регресійні коефіцієнти. Рівняння (1.2.2) відоме як лінійна функція популяції регресії (linear роpulation regression function) або просто лінійна регресія популяції. Є й інші терміни, що використовуються в літературі, - лінійна регресійна модель популяції або лінійне рівняння регресії популяції. Надалі ми використовуватимемо як синоніми терміни “регресія”, “рівняння регресії” і “регресійна модель”.

У регресійному аналізі нас цікавитиме обчислення PRF у вигляді (1.2.2), тобто обчислення значень невідомих b₁ і b₂ на основі наявних даних спостережень Y і X.

1.3. Значення терміна “лінійність”

Оскільки ми надалі застосовуватимемо лінійну модель вигляду (1.2.2), важливо визначити точний зміст терміна «лінійний», оскільки можливі дві різні його інтерпретації.