Доверительные интервалы статистических параметров
Ценность статистически обработанных данных вариационного ряда заключается также и в том, что вычисленные средние арифметические, а так же коэффициенты вариации, коэффициенты корреляции, критерии различия и другие показатели получают количественные границы доверия. Границы доверия обозначают возможные колебания статистических показателей в меньшую и большую стороны в пределах доверительного интервала. В зависимости от типа распределения данных доверительный интервал может быть определен двумя способами.
1. В симметричных распределениях, близких к нормальному распределению, размах отклонений от средней арифметической обычно равен 3 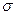 . Отклонения от средней арифметической, для их сравнения, выражают в долях сигмы
. Отклонения от средней арифметической, для их сравнения, выражают в долях сигмы 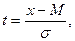 где t – нормированное отклонение от средней арифметической, х – любая варианта совокупности, М – средняя арифметическая,
где t – нормированное отклонение от средней арифметической, х – любая варианта совокупности, М – средняя арифметическая, 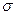 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
При расчете доверительного интервала для трех стандартных доверительных уровней: Р1=95%, Р2= 99%, Р3= 99,9%, t выбирается по таблице значений критерия Стьюдента, по числу степеней свободы, соответствующему данному параметру. Если объем выборок достаточно велик, то принимается t равные: 1,960; 2,576; 3,291, или округленно: 2,0; 2,6; 3,3 по тем же доверительным уровням, то есть берется последняя строка таблицы (Приложение, табл. 3).
Доверительный интервал средней арифметической строится: М – t mM < истинное значение < M+tmM.
Для вариационного ряда, отражающего даты зацветания клена Генри, доверительный интервал средней арифметической построим на 95% уровне, при числе степеней свободы v = 14-1=13, откуда по таблице Стьюдента t= 2,160. Средняя арифметическая М = 74,9, ее ошибка mM = 1,9, следовательно: 74,9 – 2,160 х 1,9 < истинное значение < 74,9+ 2,160 х 1,9, то есть истинное значение средней арифметической даты зацветания клена Генри находится в пределах не меньше 70,796 и не больше 79,004. Переведя данные значения в календарные даты можно записать, что дата зацветания этого вида находится между 9 мая и 18 мая.
Подставив в формулу вместо средней арифметической и ошибки средней арифметической величину любого параметра и его ошибки, можно построить для них доверительный интервал и, таким образом, оценить эти параметры.
Когда доверительный интервал необходимо построить при неизвестном типе распределения вариант, применяется неравенство Чебышева. В этом случае подразумевается, что размах отклонений от средней арифметической в совокупности с неизвестным распределением может быть больше, чем в нормальном распределении, то есть больше чем три сигмы. Согласно неравенства Чебышева истинная средняя арифметическая находится в интервале:
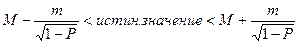 , где М - средняя арифметическая, рассчитанная по выборке; m M - ее ошибка; Р - доверительный уровень в долях единицы или 1-Р = W - уровень значимости.
, где М - средняя арифметическая, рассчитанная по выборке; m M - ее ошибка; Р - доверительный уровень в долях единицы или 1-Р = W - уровень значимости.
Построим доверительный интервал для средней арифметической из нашего примера по неравенству Чебышева: M=74,9; mM=1,9; примем доверительный уровень Р = 95%, то есть уровень значимости W = 1-P1 = 1-0,95 = 0,05. По формуле определяем: 74,9 - 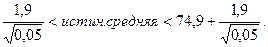
Следовательно, согласно неравенству, средняя арифметическая с вероятностью 0,95 находится в пределах от 66,4 до 83,4, то есть в более широком интервале, чем при нормальном распределении.
Дата добавления: 2020-10-25; просмотров: 795;











