Способом условной средней (даты зацветания К. Генри- A. henryi Pax.)
| Даты (х) | а= х - А | а2 | Даты (х) | а=х-А | а2 |
| -10 | -2 | ||||
| -8 | -2 | ||||
| -6 | +3 | ||||
| -5 | +6 | ||||
| -4 | +10 | ||||
| -3 | +11 | ||||
| -3 | +12 | ||||
| ∑=1049 | ∑= -1 | ∑=677 |
Суммируем варианты вариационного ранжированного ряда (столбцы 1,1) и делим сумму на число наблюдений. В результате получаем значение средней арифметической (М). Формула вычисления средней арифметической: 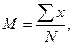 где
где 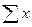 - сумма вариант, N - объем выборки.
- сумма вариант, N - объем выборки.
Для нашего вариационного ряда: 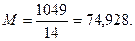
Для вычисления среднего квадратического отклонения воспользуемся методом условной средней.
Ближайшее к М (средней арифметической) целое число А = 75. Используем это число в качестве условной средней (А). Отклонения от условной средней получаем по формуле: а = х – А (столбцы 2 и 2 в табл. 1). Например, для минимальной варианты из нашего вариационного ряда, значение которой составляет 65, отклонение (а) от условной средней А (75) будет составлять в соответствии с формулой: а = 65 – 75 = - 10. Вычисляем остальные значения отклонений и вносим их в столбцы 2 и 2. Суммируем отклонения с учетом их знаков. В результате получаем сумму отклонений: ∑ а = (-43) - (+42) = (- 1).
Правильность вычислений определяем по формуле: ∑а =∑х – NA, где а - отклонения от условной средней арифметической, х – значение вариант, N- количество вариант (объем выборки), А- условно средняя арифметическая. Подставляя в уравнение значения, получаем: -1 = 1049 - 14 х 75 = -1. Таким образом, равенство обеих частей уравнения соблюдается, следовательно, вычисления выполнены правильно.
Возводим в квадрат условные отклонения и отклонения в квадрате вносим в столбцы 3 и 3 табл.1. Отклонения, возведенные в квадрат, Суммируем. В результате получаем: ∑ а2 = 677.
Среднее квадратическое отклонение определяем по формуле:
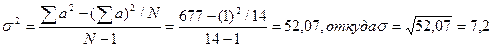
Определяем остальные параметры для нашего не взвешенного ряда по уже известным формулам, а для определения ошибок этих параметров формулы приводим, непосредственно, при их вычислении:
Ошибка средней арифметической: 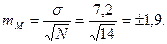
Критерий достоверности средней арифметической: 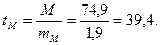
Ошибка сигмы определяется по формуле: 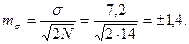
Коэффициент вариации: 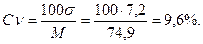
Ошибка коэффициента вариации определяется по формуле:
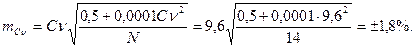
Показатель точности опыта: 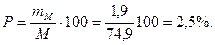
Ошибка показателя точности опыта определяется по формуле:
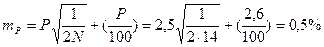 .
.
Медиану (Ме) определяем следующим образом: находим номер медианной варианты, который равен: 0,5(N+1)= 0,5 (14+1) =7,5. При четном числе вариант за медиану принимается середина промежутка между двумя центральными вариантами. При нечетном числе вариант за медиану принимается центральная варианта. В нашем случае, при четном числе вариант, медиана равна полусумме вариант 7 и 8: Ме = (72+73) / 2=72,5.
В результате мы получили основные параметры, дающие довольно полное представление о данном вариационном не взвешенном ряде. Истолковать результаты статистических исследований можно примерно так: в среднем за 14 лет клен Генри зацветает через 74,9 дня от первого марта, то есть округленно 14 мая, с ошибкой в 1,9 дня. Варьирование годовых дат зацветания у этого вида сравнительно невелико, так как коэффициент вариации равен 9,6± 1,8%. Полученные параметры заслуживают доверия ввиду большой достоверности средней арифметической (t = 39,4, что >3) и значения показателя точности опыта меньшего 5% ( Р=2,5±0,5% < 5%).
Дата добавления: 2020-10-25; просмотров: 614;











