Высота растений А. высочайшего (A. altissima Swingle) в опыте (см)
| 218,6 | 219,2 | 219,2 | 220,2 | 220,2 | 221,3 | 221,4 | 221,5 | 221,6 | |
| 222,1 | 222,8 | 223,2 | 223,4 | 223,5 | 224,1 | 224,1 | 224,2 | 224,3 | 225,2 |
| 225,2 | 225,3 | 225,4 | 225,4 | 225,6 | 225,8 | 226,3 | 226,3 | 226,3 | 226,3 |
| 226,3 | 226,3 | 227,3 | 227,3 | 227,3 | 227,3 | 227,4 | 227,8 | 227,8 | 227,9 |
| 228,1 | 228,1 | 228,2 | 228,3 | 228,4 | 228,4 | 228,5 | 228,6 | 229,1 | 229,1 |
| 229,1 | 229,2 | 229,3 | 229,3 | 229,4 | 229,5 | 229,6 | 229,7 | 230,1 | 230,4 |
| 230,5 | 230,5 | 230,6 | 230,7 | 230,8 | 230,8 | 230,9 | 230,9 | 231,2 | 231,2 |
| 231,2 | 231,3 | 231,3 | 231,5 | 321,6 | 231,7 | 231,8 | 231,8 | 231,9 | 232,3 |
| 232,4 | 232,5 | 232,5 | 233,5 | 233,5 | 233,5 | 233,6 | 233,6 | 234,1 | 234,2 |
| 234,3 | 234,4 | 234,4 | 235,5 | 236,6 | 236,6 | 237,3 | 237,5 | 238,8 | 240,0 |
N=100
Приводим данные рядов (табл.2, 3) в виде ранжированных взвешенных вариационных рядов (табл. 4 - 5).
Для этой цели определяем величины классовых интервалов, зависящих от принятого числа классов и объема выборок. Для объема выборок из 100 вариант по таблице определяем, что число классов равно восьми. Тогда классовые интервалы выборок будут равны:
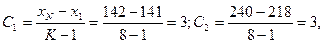 где С – величина классового интервала; ХN – величина максимальной варианты выборки; Х1 - величина минимальной варианты выборки (в контроле, соответственно, 141 и 121; в опыте- 240 и 218 см); К – число классов, принимаемое обычно от 7 до 18. В нашем случае число классов составляет 8.
где С – величина классового интервала; ХN – величина максимальной варианты выборки; Х1 - величина минимальной варианты выборки (в контроле, соответственно, 141 и 121; в опыте- 240 и 218 см); К – число классов, принимаемое обычно от 7 до 18. В нашем случае число классов составляет 8.
Расчет границ классов начинается таким образом, чтобы полученные средние значения классов были по возможности малозначными числами. В нашем случае для контроля произвольным числом нижней границы первого класса выбираем 120 см, а для опыта 217 см., т. е. на один см меньше минимальных вариант. К этим числам прибавляем величину классового интервала (С= 3 см). Получаем верхнюю границу классового интервала (табл. 3- 4, столбец 1). Для удобства распределения вариант по классам мы несколько уменьшаем значение верхней границы классового интервала. Например, для контроля фактические границы первого класса будут 120 и 123, а мы в табл. 3 записываем 120 - 122,9, в этом случае следующий класс начинается с числа 123 и, соответственно, заканчивается числом 125,9. Для первого класса начало отсчета границы желательно выбирать так, чтобы крайние варианты (Х1 и ХN) оказались ближе к середине своих классовых интервалов. Срединные значения для первого класса в табл. 3 и табл. 4 вычисляем следующим образом:
для контроля (120 +123): 2=121,5; для опыта: (217+220):2=218,5.
Все остальные срединные значения классовых интервалов получаем путем последовательного прибавления к ним величины классового интервала. Середины классов рассматриваются как варианты ряда и обозначаются через Х. Число вариант относящихся к данному классу, называется его частотой. Например, в табл. 3 класс 120-122,9 имеет частоту 5, т. е. в этот класс вошли варианты из табл. 2: 121, 121,1, 121,1, 122,3 и 122,3. Частоты вариант, выраженные в процентах от общего числа вариант выборки или, как доли единицы, называются частостями. Частости отражены в табл. 4 и 5, столбец 4. Распределение (разноска) вариант по классам и составление, таким образом, взвешенного вариационного ряда в значительной степени упрощает последующие вычисления статистических параметров, характеризующих среднюю арифметическую, вариационный ряд и генеральную совокупность, являющуюся объектом изучения. Взвешенный вариационный ряд целесообразно составлять при объеме выборки, насчитывающем более 50 вариант. Процесс составления взвешенных вариационных рядов программируется и может быть выполнен с использованием ЭВМ.
Таблица 4
Дата добавления: 2020-10-25; просмотров: 617;











